untitled (5) (pdf.file)

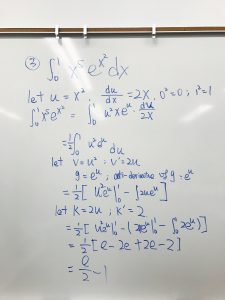
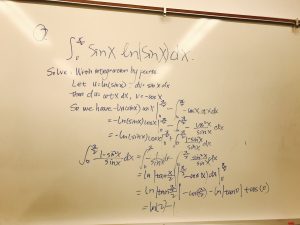
Here’s the question&solution code for overleaf user:

\documentclass{article}
\usepackage[utf8]{inputenc}
\begin{document}

\bigskip

1. calculate $\displaystyle\int_0^1 x^5e^{x^2}dx$

\bigskip

Let $u=x^2$, $\frac{du}{dx}=2x$, $0^2=0$, and $1^2=1$

\bigskip

$\displaystyle\int_0^1 x^5e^{x^2}dx=\displaystyle\int_0^1 u^2xe^u\frac{du}{2x}=\frac{1}{2}\displaystyle\int_0^1 u^2e^udu$

\bigskip

Let $v=u^2, v’=2u, g=e^u$, and anti-derivative of $g=e^u$, then the function will be $\frac{1}{2}[u^2e^u\big|_0^1-\displaystyle\int_0^1 2ue^u]$

\bigskip

Let $k=2u,k’=2$, then the function will be $\frac{1}{2}[e-2e+2e-2]=\frac{e}{2}-1$
\bigskip

\bigskip

2.calculate $\int_{0}^{3} (2x^3+18x)sin(x^2+9)dx$
\bigskip

$=\int_{0}^{3} 2x(x^2+9)sin(x^2+9)dx$
\bigskip

According to substitution method
\bigskip

let $w=x^2+9, dw=2x$
\bigskip

$=\int_{9}^{18} w\cdot sin(w)dw$
\bigskip

According to integration by part method
\bigskip

let $u=w, du=dw, v’= sin(w)dw, v=-cos(w)$
\bigskip

$= -cos(w)w|_9^{18}- \int_{9}^{18} -cos(w)dw$
\bigskip

$= -cos(w)w|_9^{18} +sin(w)|_9^{18}$
\bigskip

$=sin(18)-sin(9)-18cos(18)+9cos(9)$
\bigskip

\bigskip

3. calculate $\displaystyle\int_0^{\frac{\pi}{2}}sinx lnsinx dx$

Solve: With integration by parts. Let u=$lnsinx$, $dv=sinxdx$
\bigskip

Then $du=cotxdx$, $v=-cosx$
\bigskip

So we have that $-ln(sinx)cosx|_0^{\frac{\pi}{2}}-\displaystyle\int_0^{\frac{\pi}{2}}(-cosxcotxdx)$=$-ln(sinx)cosx|_0^{\frac{\pi}{2}}$-$\displaystyle\int_0^{\frac{\pi}{2}}\frac{1-sin^{2}x}{sinx}dx$
\bigskip

$\displaystyle\int_0^{\frac{\pi}{2}}\frac{1-sin^{2}x}{sinx}dx$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{1}{sinx}$-$\displaystyle\int_0^{\frac{\pi}{2}}\frac{sin^{2}x}{sinx}$=$ln|tan\frac{\pi}{4}|-cos\frac{\pi}{2}-ln|tan0|+cos0$
\bigskip

=$ln(2)$-1

\end{document}