Antiderivative

If we know the derivative of a function, the process that we try to find its origin function is the antiderivative.

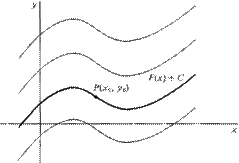
However, the derivative of a constant is 0, we can not determine which constant is in the origin function, so we can just find a set of functions which all have a derivative like this.

For instance, if f(t)=t is the derivative of F(x)

We need to figure out which function has a derivative equal to t.

By doing the opposite operation of differentiation, it is easy to find out one of the origin function F(t)= ½ t^2

As we know, the derivative of a constant is 0, so we can not determine what the certain original function is. In fact, all the function F (t)=½ t^2 +C (C can be any number) have a derivative equal to f(t)

Integration

Integration can be classified into definite integration and indefinite integration. Indefinite integration exactly has the same meaning of antiderivative. The indefinite integration of a function f, which is also known as the antiderivative of a function f, is a function F such that F′=f, while the definite integral is just a number. The definite integration of a function is equal to the area under the function on a certain domain.

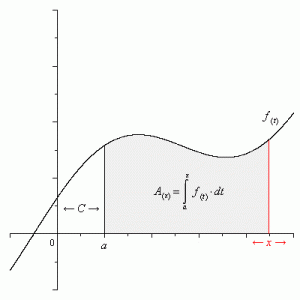
As the picture shows above, the grey part is the indefinite integral of the function f (t).

If we replace variate twith a certain number, it becomes the definite integration of the function f (t).

If we want to find the area of the UBC fountain without using π, how can we do just with the radius r?

We can regard this fountain as a circle.

The question is, without π, just with radius r, how can we get the area of a circle?

First, we divide this circle into eight parts and calculate the area of these four triangles. Then, we can roughly get the area of the circle.

Then, I divide this circle into sixteen parts, only regard the area of these eight triangle as the area of circle, we can find the “extra” area is smaller than last graph.

Then, we make a hypothesis that, if we can divide this circle into 2n parts, regard the area of the triangle as the area of circle, the “extra” area will become smaller and smaller, and our result will be more precise.

The process like this is also like the process of integration.

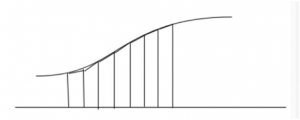
But the difference is, if we want to integrate a function, we need to cut the area ,which is between x axis and the curve, into many pieces and calculate the area of each pieces and add them together. If the number of pieces is big enough, we will get more precise number of the area between x axis and the curve.

For the question four in the midterm, the most important point is to remember and understand every test of the convergence of the series clearly. Based on the theory, the second step is to link (a) and (b) together can connect to the (c). The tricky part of this question is you can treat the graph of (a) and (b) as the front elevation and the vertical elevation of a cuboid. They have a different length side, but also have a same length side which connect them.

(a) What distinguishes convergent sequences from divergent sequences

Convergent sequences: One day, a super virus appears. This super virus not only can make everything die, but also can eat everything to grow up. Because of the super virus unlimited devour, all the people, animals, plants even bacteria extinct. The super virus has nothing to eat. So, the only way for the super virus to keep alive is to eat itself. During the first day, half of the super virus eats the other half of the super virus. And in the second day, half of the half of the super virus eats the other half of the half of the super virus. The amount of the super virus in everyday is a convergent sequence.

Divergent sequence: From now on, let us calculate the time just pass by which is 1s, 2s, 3s…. Although we can continue calculate, there will have no end for the time. And the time is a divergent sequences.

(b) What distinguishes convergent series from divergent series

Convergent series: Image a young woman win 1,000,000,000$. She was so excited about this, but she was also too young to plan how to use these money. So she decided to use the half of the money for her whole life. But time is so fast. She runs out of the half of the money in one year. Because she also cannot believe the truth, she learns to plan the money. But she till runs out of the one fourth of the money in the second year. After many years, she still uses the half and the half and the half and …… of the 1,000,000,000$. The amount of the money that she used after she won the prize is a convergent series.

Divergent series: A person is so lazy. But he wants to build a stone house by himself. So he creates a plan: bring one stone back to home everyday. So, in the first day, this person gets one stone. And in the second day, this person gets one plus one which is two stones and so on. The amount of the stones that this person have is a divergent series.

Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!