Term: Universal Turing Machine

Introduction:

The objective of this assignment is to learn how to write the definition of a relatively complex term for an audience that may not fully know the technical meaning of the term. The criteria include choosing a non-technical audience and writing three different types of definitions: parenthetical, sentence, and expanded. Furthermore, four expansion strategies must be used with one of them being visual representation.

The audience for people who do not understand how computers work. I first explain what Turing Machines are and then proceed to explain the existence of a particular Turing Machine called the Universal Turing Machine. I hope to provide the reader with a better understanding of why modern computers work in the way they do.

Parenthetical Definition:

In 1937 Alan Turing discovered the Universal Turing Machine (a computer).

Sentence Definition:

The Universal Turing Machine is a Turing machine that simulate any other Turing machine. It does this by reading both the description of a Turing machine to be simulated as well the input from its own input.

 

Expanded Definition:

To understand the Universal Turing Machine, we must first understand what a Turing Machine is. A Turing machine consists of a blank tape going infinitely in both directions. It also has a scanner that reads the current symbol on the tape and a set of instructions that tell it what to do depending on the state it currently is in. A simple representation of this is as follows:

 

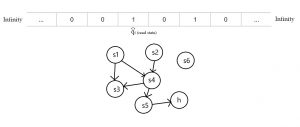
The set of instructions is the key for making computations. Depending on whether the scanner reads a 1 or a 0, the instructions can tell the scanner to do one of four operations: print a 1, print a 0, move one block left, or move one block right. With only these simple set of instructions we are able to construct Turing Machines that can solve functions. Here is an example of a Turing Machine that calculates f(x) = x + 1 where in this case x=4.

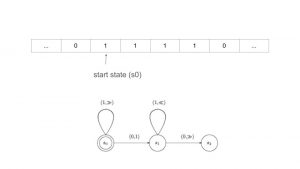
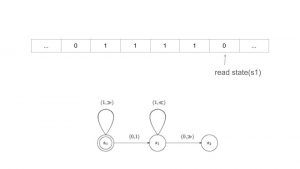
We can see the scanner reads a 1 it moves one to the right and returns to S0. It continues to do so until the scanner reads a 0 and then proceeds to print a 1 to produce the output 4+1. It then moves back into its starting position.

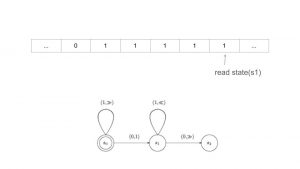
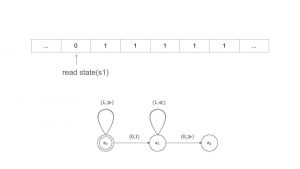
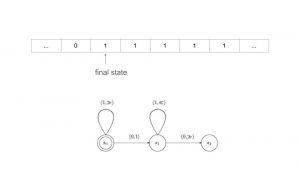
We can also use Turing Machines to calculate other functions. Here is one for f(x, y) = x + y where x=2 and y=3.

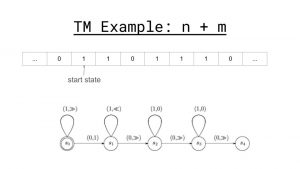
We can also using the Turing Machines to calculate other functions as well such as f(x) = x^2, f(x) = x/y, f(x) = x^7 + y^2 + z ^6, and so on. In fact the Church-Turing thesis states that every function that can possibly be computed can be solved by a Turing Machine.
Another remarkable feature of Turing Machines that Turing discovered is the fact that it is possible to assign each Machine it’s own unique number. To see this let us rewrite the state map for f(x) = x + 1 to a set of 4 tuples like so:

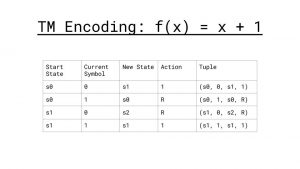
We can now encode this machine to a binary number by having four blocks of 1’s each separated by a 0. The first block is the number of the start state, the second block represents whether the current symbol is a 1 or a 0 (using 1 to represent 0 and 11 to represent 1), the third block represents the new state, and the fourth block represents the action the machine performs (1 for print 0, 11 for print 1, 111 for move left, and 1111 for move right. We then separate each tuple by 00 to produce a unique number for the Turing Machine.    

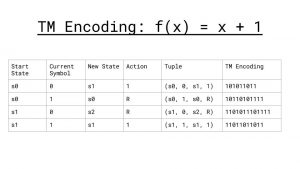
Finally we can also represent the input by separating it with a block of three 000’s. Here is the final binary number for the function f(x) = x +1 where x =4.

 

If we express this binary number in integer form it would be:

 

Now that we have a unique number for every Turing Machine M, it follows that there is another Turing Machine U that simulate any machine M. This can be represented as follow U = <M, x>. What this means is that when we input the unique number for f(x) = x + 1 where x = 4 the output of U will be the answer to the function. It can be visualized like so:  U<97721817568079247> = 5. We can also input the unique numbers for f(x, y) = x + y, f(x) = x^2, f(x) = x/y, and any other function that can possibly be computed. While there are functions it can’t compute, such as the Halting Problem, it nevertheless can solve every other problem, which there happen to be an infinite amount of. As every modern computer is a Universal Turing Machine, this gives us some insight into why computers are so powerful.