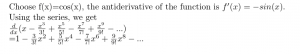
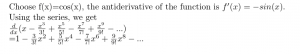
Vissage Bai 32204166

Penny Pan 17757162

Yue Deng 56890163

Ding Cheng 21768163

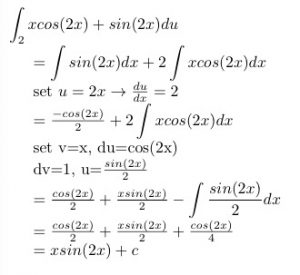
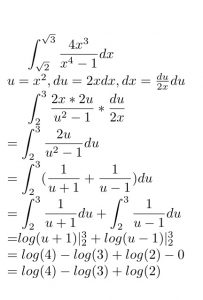
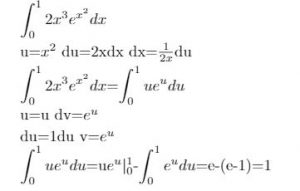
Vissage Bai 32204166

Penny Pan 17757162

Yue Deng 56890163

Ding Cheng 21768163

Antidifferentiation，also known as indefinite integration， is the antiderivative calculation. Indefinite integral is the inverse of differential that produce a formula.

Integration calculates a specific value. Unlike Antidifferentiation, it produce  a specific number. However， they have some connections. As integration is a process of calculate the aera of its antiderivative, integration is somehow based on antidifferentiation. After get a fuction’s antidifferentiation, by puting the restriction number in the both sides of the interval, we can get the integration in that interval.

To sum up, the definite integral is limited by the numbers on both sides of the interval, and the indefinite integral is not limited by numbers. They are all calculation process, producing different things. But Indefinite integral is the basis of definite integral.

For example, the antiderivative of the function, F(x)= is f(x)=, c is a constant. The constant is hard to calculate. Therefore, the antiderivative of the function is a function, not a excact value. In contrast, definite integral has an interval. For instance, the  is equal to . Because the definite integral is between two numbers, the definite integration of a function would produce a specific number.

Integration would be divided into two parts, indefinite integration and definite integration. Antidifferntiation is belong one of part of the integration, which is indefinite integration.

Vissage Bai 32204166

Penny Pan 17757162

Yue Deng 56890163

Ding Cheng 21768163

Integration is the area under a smooth curve in calculus, which could be applied in the real world. The area under the curve could be divided into lots of rectangles that are parallel to the y-axis. Then, pulsing the rectangles, which is the area of the curve.

Even though the method of integration is widely applied in the field of Physics, Engineering, and Astronomy, the idea of integration was first invented by ancient Greek scientist Eudoxus. Surprisingly, in the far east, the idea of integration also emerged in China, which was proposed by Zu Chongzhi. He used integration to calculate the total area of circles, which is very like the modern integration method.  However, most of these theories are not vigorous, which cannot be applied in the daily life. After hundreds of years, Isaac Newton, another famous mathematician in England, published his book The Principia, which better explains and perfects the idea of integration. This book had profound impact in that era. Breakthrough in fields of navigation, astronomy and mechanical system were made by other scientists using the Newton’s new idea of integration. Until now, integration is still an important part of the subject of Calculus.

Integration can apply in other areas. For example, in physics, integration is used to calculus the relationship between displacement, velocity and acceleration. When students are given the velocity of an object, displacement can be calculus by using integration. And velocity also can be calculus by using it when acceleration is given. Because acceleration is the derivative of velocity and velocity is the derivative of displacement. And in mathematics, derivative is related to integration. Integration also can be used in the life. A computer, it consumes electricity when it is opening, but it is difficult to calculus the average electricity consumption of it. Then integration can be used. After getting the graph of electricity consumption each time, the total electricity consumption can be calculus by using the knowledge of integration. Next average consumption can be known. That helps computer company design better computers which use less electricity. There are extra applications of integration in other subject and in the life. Integration is helpful for science and life applications.

this question is a question about limit

at first，we should know how to express the area by a mathematical equation.

then, we can find the rule of the equation.

it is a geomatric sequence, and we can use the knowledge of limit to find the limit of this seuence, then we can solve this question.

convergent sequence is a sequence when n closes to infinite, the evaluate of sequence closes to a natural number which less than infinite. For example, {1,1/2,1/3,1/4,1/5,1/6…….1/n}

divergent sequence is a sequence when n closes to infinite, the evaluate of this sequence is infinite. for example，{1,4,9,16,25,36…….n^2}

convergent series is a series that the sum of this series is closes to a number which is less than infinite. For example, the sum of 1/n^2

divergent series is a series that the sum of this series is infinite, for example, the sum of 1/n

Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!