1.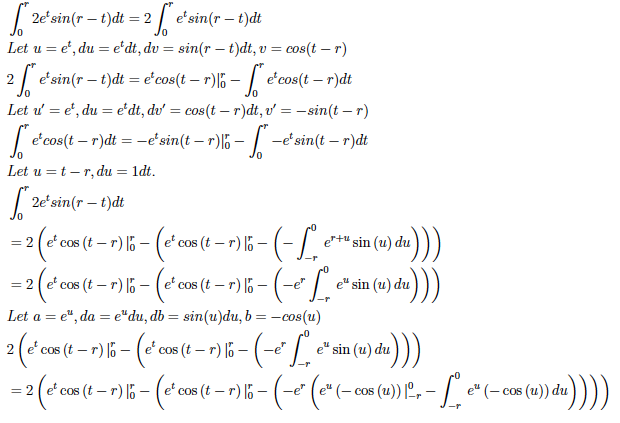
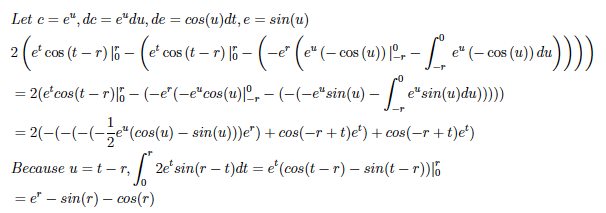
2.3.
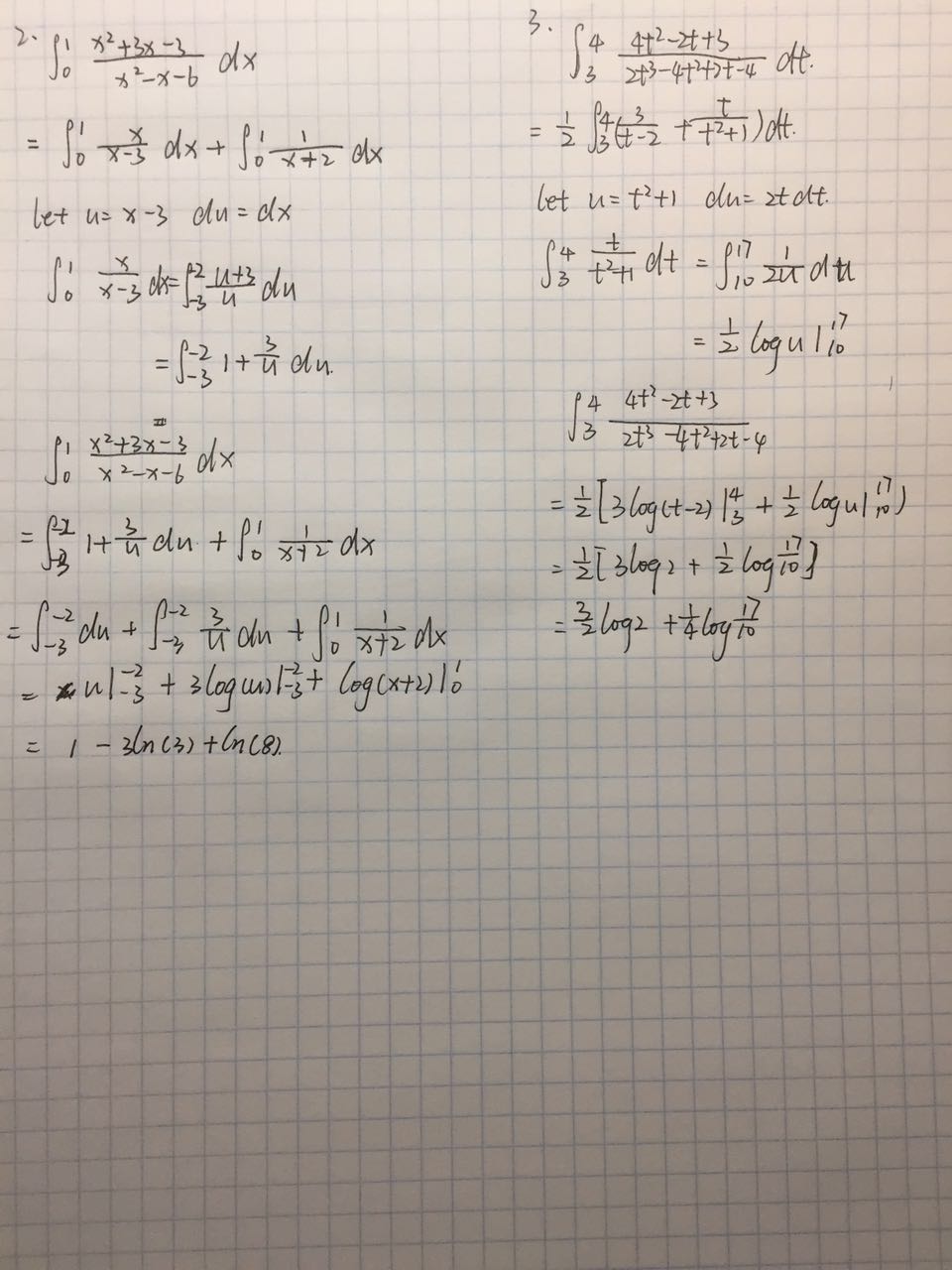
1.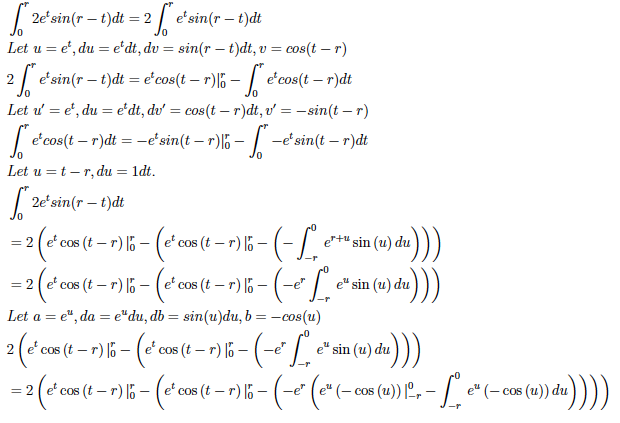
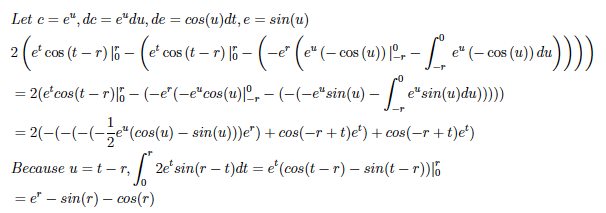
2.3.
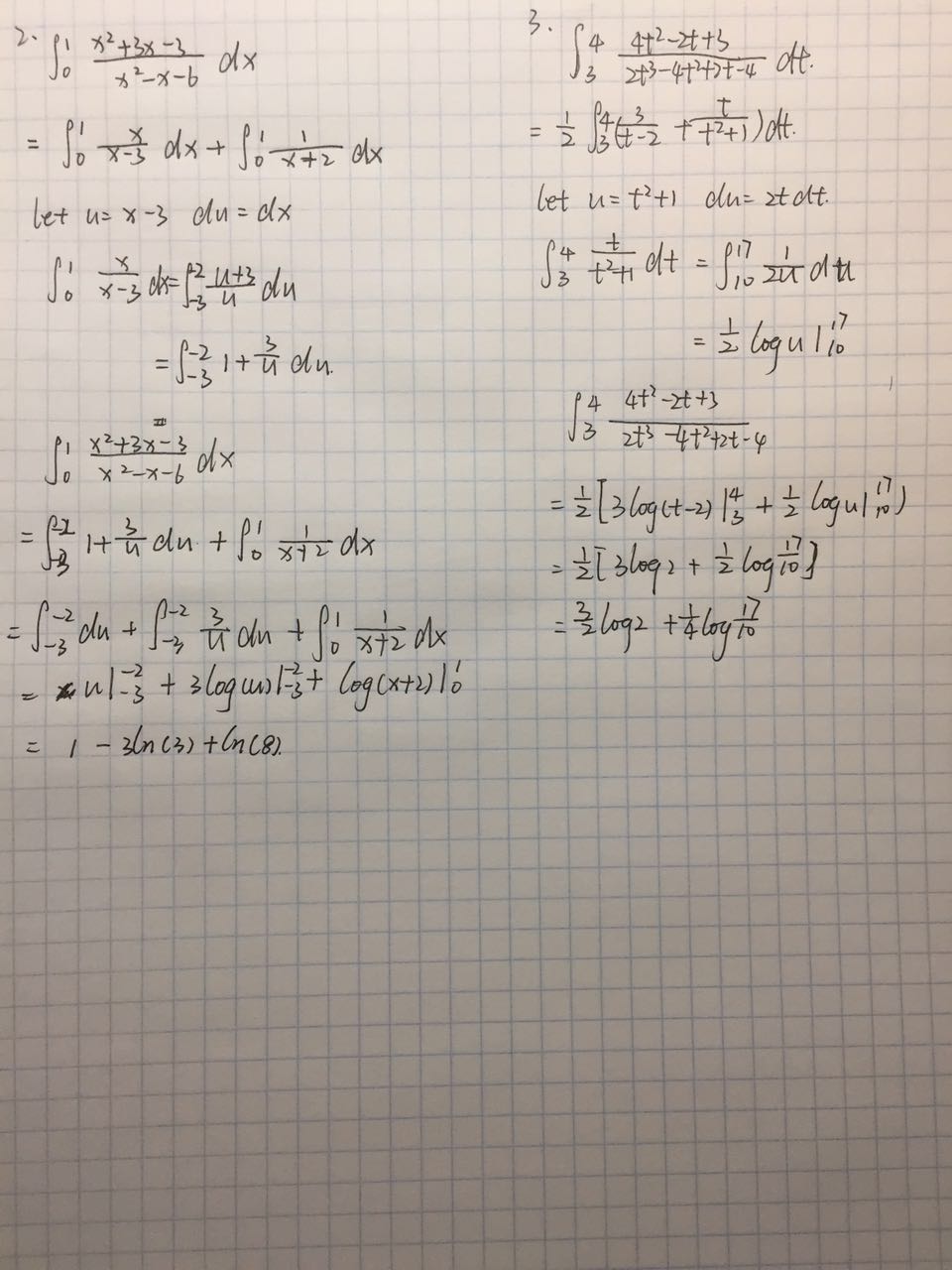
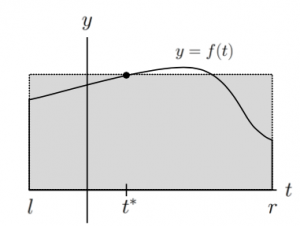
For the deeper and more precise calculation, we divide the interval [r-l] into three equal sub-intervals like t1, t2 and t3.
Then t1=t2=t3=(r-l)/3.
And we find three number t1*, t2* and t3* which within three sub-intervals respectively, calculating their value of y-axis such as f(t1*), f(t2*) and f(t3*)
Therefore, the refined area under the function can be presented as A=f(t1*)·t1+f(t2*)·t2+f(t3*)·t3
With this trial, we can divide [l,r] into more and more sub-intervals to reach the most precise area that I want to calculate.
Of course, area only can be calculated in some functions like continuous functions, for the reason that a non-continuous function does not have closed area.
Written by Yuki Zhang(50653161) and Denise Wang(24482168)
I solved the Question 5, and I found the secret of this question.
We can know the general formula of the area is removed in each step. We treat the general formula as a series.Then the sum of the series is the area which has been removed. By the knowledge we have learned about the series. We can know the sum of this series when n approaches a large number which approaches to a constant.Then we know the Sierpinski carpet, and we can solve the question.
I think we need to transfer the questions to the knowledge we have learned.
Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!