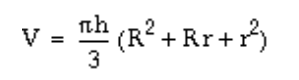Math Games
Here is a list of math games that my colleagues and I have developed throughout this education program
Math Problem 1
Volume of a Pyramid Frustum
Background of the Problem
Usually when Egyptians calculated volumes, they mainly used cuboid shaped or cylindrical containers. However, we also know that Egyptians made pyramids from the bottom to the top, so they must of some aspect knew how to calculate the volume of a square truncated pyramid. In fact, a similar question to the square truncated pyramid actually appears as problem 14 of the Moscow Mathematical Papyrus. The question was stated as follows:
“If you are told: a truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top: you are to square the 4; result 16. You are to double 4; result 8. You are to square this 2; result 4. You are to add the 16 and the 8 and the 4; result 28. You are to take 1/3 of 6; result 2. You are to take 28 twice; result 56. See, it is of 56. You will find [it] right”
Translating this text in modern English becomes this:
“a pyramid has been truncated in such a way that the top area is a square of length 2 units, the bottom a square of length 4 units, and the height 6 units, as shown. The volume is found to be 56 cubic units, which is correct.
However, there was no proof that Egyptians ever found this formula. However, they did use a way to approximate it, which was estimating the base as B=(1/2)(a^2+b^2), and so the volume would be V=(h/2)(a^2+b^2). Kurt Vogel thinks that the Egyptians must of realized this mistake, so they added an extra median area unit ab into the formula to approximate it even more accurately. However, the approximation actually is the exact value, thus they discovered the correct formula.
Problem
So the question is as follows.
For a more visual understanding of the problem, we visualize the following picture:
The Main Solution
At first, we calculate the volume of the cuboids, 4 lateral rest prism, and 4 corner pyramids individually. However, there is no formula to really calculate the volume of the corner pyramids. So we used the volume of a square pyramids instead. Then we added everything up.
We also decided to treat the corner pyramids as triangular prisms. However, doing so and adding up all the volumes actually ends up giving you the approximation of the volume of the square truncated pyramid that Egyptians used V=(h/2)(a^2+b^2).
Alternate Solution
Now instead of splitting it into parts like the question said, we decided to calculate the volume of the missing part pyramid, and the volume of the whole pyramid. Then we subtracted them to get the truncated square pyramid.
Extension of the Problem
Using the alternate solution we found, we can actually extend this to cone frustums. Just like pyramid frustums, they are cut off from the top. Can you find the volume of a cone frustum?
You should arrive at this formula: