There are rules if you want to succeed in this class. Clarissa Audrey (51844165), Mariana Paspuel (44069169), Tong Cui/Chelsea (31032162), Hongjiang Ye/Violet (52433166) present to you these guidelines, follow them (and some lucks) and you may be the top star!

1. If you’re confused, don’t be embarrassed to ask simple math question, like

<img src=”http://i.imgur.com/ERUU04C.jpg” width=”500″ height=”281″ class=”aligncenter size-medium” />

Seriously, don’t wait until last minute to ask, you might (and always) forget.

2. If you wanna skip, skip the lecture, not the tutorial

<img src=”https://31.media.tumblr.com/ff2c770cfbfe09b1bb9a888039acfffc/tumblr_inline_nkxaodDQ5c1qf4j1l.gif” width=”500″ height=”278″ class=”aligncenter size-medium” />

Tips: Work best if you don’t skip at all.

3. Late to class? It’s better late than…

<img src=”http://25.media.tumblr.com/3e1beb1a73fd22d081ee635c10080bb5/tumblr_muhajrF8Cb1si6qheo1_400.gif” width=”350″ height=”224″ class=”aligncenter size-medium” />

…never

4. Office hour is “ask everything you want” time

<img src=”https://az616578.vo.msecnd.net/files/2015/02/10/635591909975691405478466399_200-4.gif” width=”327″ height=”200″ class=”aligncenter size-medium” />

5. If you’re looking at your homework like this

<img src=”https://media.giphy.com/media/uaULFlGTpyrNm/giphy.gif” width=”375″ height=”217″ class=”aligncenter size-medium” />

or like this

<img src=”https://ssdiaries.files.wordpress.com/2014/12/giphy-45.gif?w=676” width=”500″ height=”270″ class=”aligncenter size-medium” />

come for help!

6. You will likely fail this class if you cheat, so don’t.

<img src=”http://2.bp.blogspot.com/-vCY876FGefQ/UQOnMc-P20I/AAAAAAAAHAs/osISNLISCuw/s1600/copy-of-a-copy.gif” width=”500″ height=”195″ class=”aligncenter size-medium” />

P.S. I never cheat and still fail this class.

7. If you fail on a test, don’t be down! Because 95% chance you’re not alone.

<img src=”https://s-media-cache-ak0.pinimg.com/originals/8b/25/14/8b2514e04629b6c666a0b0b02c9c74ef.gif” width=”500″ height=”281″ class=”aligncenter size-medium” />

One for all, all for one!!

8. The question on the test is as simple as: If John have 3 apples and Tim give him another 5 apples, then Jess eat 2 of the apples. How many apples does Terry have?

<img src=”https://media.giphy.com/media/5yLgoczEvFoE5LyoiZO/giphy.gif” width=”556″ height=”242″ class=”aligncenter size-medium” />

Who the hell is Terry?

<img src=”https://media.giphy.com/media/h4Z6RfuQycdiM/giphy.gif” width=”500″ height=”281″ class=”aligncenter size-medium” />

Seriously, most of the exam questions don’t make sense at all.

9. If you don’t know what to write, just write anything you know

<img src=”https://az616578.vo.msecnd.net/files/2016/11/22/6361544690707084141513950022_giphy.gif” width=”500″ height=”300″ class=”aligncenter size-medium” />

<img src=”http://media.thedailytouch.com/2015/11/Writing6.gif” width=”500″ height=”244″ class=”aligncenter size-medium” />

and may God bless the teacher who grades your test.

10. Last minute studying before exam won’t work

<img src=”http://68.media.tumblr.com/3bba5f0d6c2cfca460882a006454c128/tumblr_inline_nflyctCqiL1ravhwt.gif” width=”282″ height=”207″ class=”aligncenter size-medium” />

11. Math needs

<img src=”https://lh6.googleusercontent.com/UeG_2LQyfqv6CeT2kvZb2g1ezvwlUQItww66crYwgFgicysKkZJvPOynuL0SdEhJE_6jzHNzOmOjH9vWGJpMNc2SuWD2Y8xC14Y-eQnofL2TIhON4HBovy_s3apPH7cUEFQeGto6” width=”500″ height=”309″ class=”aligncenter size-medium” />

12. Look who were there for you when you’re at your worst. Your goddamn self.

<img src=”https://az616578.vo.msecnd.net/files/2016/02/17/6359132753501265271476181603_Talking-to-Yourself-GIF.gif” width=”490″ height=”199″ class=”aligncenter size-medium” />

So, encourage yourself!

14. Tomorrow is a mythical land, do it now.

<img src=”https://68.media.tumblr.com/409e7b0e659f46f3d4a190631f641e81/tumblr_npwq9fRJmt1tuall8o1_500.gif” width=”500″ height=”630″ class=”aligncenter size-medium” />

15. HA! You don’t realize that I skipped 13 right? Come on man, this is math. Gotta be careful with numbers.

<img src=”https://media.giphy.com/media/yRAAHNTBGegNi/giphy.gif” width=”500″ height=”275″ class=”aligncenter size-medium” />

13. Math is not always step forward. Sometimes you gotta step back to fully understand. So, here’s your 13.

<img src=”http://www.reactiongifs.com/wp-content/uploads/2013/08/step-back.gif” width=”540″ height=”309″ class=”aligncenter size-medium” />

16. Pray to Baby Jesus.

<img src=”https://m.popkey.co/a9391c/dr0JA.gif” width=”300″ height=”200″ class=”aligncenter size-medium” />

17. Piazza is there if you’re stuck on maths!

<img src=”https://media1.popsugar-assets.com/files/thumbor/PKti9i_u7KWEeD6CtR5LKH66Z2A/fit-in/1024×1024/filters:format_auto-!!-:strip_icc-!!-/2015/05/19/824/n/3019466/c72d9f13dee461b9_pizza-game-of-thrones/i/Everyone-so-jealous-you-pizza.gif” width=”500″ height=”281″ class=”aligncenter size-medium” />

18. If you’re terrified when Professors ask a question, instead of

<img src=”https://media.giphy.com/media/3Bxf4kD5L4ovK/giphy.gif” width=”400″ height=”221″ class=”aligncenter size-medium” />

Stare into their eyes

<img src=”https://az616578.vo.msecnd.net/files/2015/10/18/635807318296542136-1065644494_shy4.gif” width=”400″ height=”300″ class=”aligncenter size-medium” />

until they’re uncomfortable.

19. Enough sleep!

<img src=”http://i.amz.mshcdn.com/2Rd5SkLQX5fG83yirrInPrmjSf4=/fit-in/850×850/http%3A%2F%2Fmashable.com%2Fwp-content%2Fgallery%2F25-exhuastion-gifs-for-when-you-cant%2Fthe-simpsons-punch.gif” width=”500″ height=”330″ class=”aligncenter size-medium” />

20. There always be those students that itch you to the core. In that case,

<img src=”https://68.media.tumblr.com/a592ac230efce778d1c6a9f78bb458a5/tumblr_nng60kscOY1qk08n1o1_500.gif” width=”500″ height=”280″ class=”aligncenter size-medium” />

or in some cases,

<img src=”http://s1.scoopwhoop.com/anger/anger5.gif” width=”500″ height=”222″ class=”aligncenter size-medium” />

21. When the question is too easy, most of the time it’s because you do it wrong

<img src=”https://images.gr-assets.com/hostedimages/1412957196ra/11447839.gif” width=”500″ height=”243″ class=”aligncenter size-medium” />

22. You may look at your teachers like this

<img src=”https://media.giphy.com/media/zSgWRDLwC1mJG/200.gif” width=”355″ height=”200″ class=”aligncenter size-medium” />

But remember, they’re there to help you. Always.

<img src=”https://media.giphy.com/media/sMa83v0n55QuA/giphy.gif” width=”500″ height=”208″ class=”aligncenter size-medium” />

23. Friday Quizzes!! L Not sure if the math test was easy or I got everything wrong

<img class=”aligncenter size-medium” src=”https://media.giphy.com/media/SIzwqBY3Ogdxe/giphy.gif” width=”400″ height=”224″ />

Note: Not always Math is that hard as you think. Trust yourself!!

24.First Math class, “Limits” find epsilon and delta. What in the world is that?

<img src=”http://vignette4.wikia.nocookie.net/degrassi/images/1/1c/Scared-gif.gif/revision/latest?cb=20140814145805” width=”320″ height=”220″ class=”aligncenter size-medium” />

<img src=”http://www.gifimagesdownload.com/wp-content/uploads/2016/02/54-scared-gif-299.gif” width=”500″ height=”250″ class=”aligncenter size-medium” />

Do not scared about this, it is just two first weeks of class :’) :’)

25.Spend like 3 hours typing written assignments is totally fine at the beginning 

<img src=”https://s-media-cache-ak0.pinimg.com/originals/64/36/08/643608efbfbc492d9af3240aff67495b.gif” width=”500″ height=”309″ class=”aligncenter size-medium” />

Never ever present handwritten homework.

26. Avoiding eye contact with your instructor because you do not know the answer to the question. Usually happens!!

<img src=”http://i.imgur.com/MKUa2j7.gif” width=”500″ height=”348″ class=”aligncenter size-medium” />

Do not be scared to be wrong, that’s part of learning.

27. Do not be late for lectures, Dr. Leung will realize everything. (e-v-e-r-y-t-h-i-n-g)

<img src=”https://img.ifcdn.com/images/a50f81143b701893b31d80e17f3d69739acfd66ff2bafaf4609c1a0325039527_1.gif” width=”390″ height=”307″ class=”aligncenter size-medium” />

Consider Math as the most important course ever 

28. When you finally understand what the class was about. You are like…

<img src=”http://img.memecdn.com/when-i-understand-something-in-math-class_o_750640.gif” width=”500″ height=”254″ class=”aligncenter size-medium” />

Keep trying and always give your best.

29. When you don’t know how to start written homework. Try!! Is not difficult as it looks.

<img src=”http://i.imgur.com/ABtwP3k.gif” width=”500″ height=”228″ class=”aligncenter size-medium” />

30. When your instructor says that the power series (1/n^2)= (pi^2/6) and you need to used the Taylor series of sin(x). You are like…

<img src=”https://media.giphy.com/media/5eqG9dkr6N6wM/giphy.gif” width=”362″ height=”204″ class=”aligncenter size-medium” />

Assigment_7 q3

Clarissa Audrey 51844165

Mariana Paspuel 44069169

Violet Ye 52433166

Tong Cui （Chelsea) 31032162

untitled (1)9999

Tong Cui (Chelsea)

The simplest way to answer this is by saying that integration is a way of adding small slices or small parts to find the whole. And it can be used to find areas, volumes, and central points of many things. So, how can we use those slices to find the area or volume? Imagine that we have a glass and tap water. Integration is like filling the glass from a tap. Adding up the little bits of water to the bucket gives us the volume of water in the bucket.

In more mathematical way, if we are being asked to find the area of a triangle or a circle or a square, it’s easy since we already know the formula of those shapes. But, imagine if we are being asked to find area of irregular shapes, e.g an irregular curve.

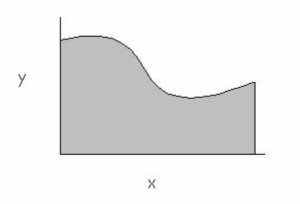
A good starting point will be to draw rectangles in the area of this shape because as we said before, we already knew how to calculate the area of the basic shapes.
Then, we can calculate the area of both rectangles and add them together. However, to be noted, the problem with this method is that it’s only a rough approximation of the area (not the factual area).

So, the solution is to make the rectangles narrower as you can see in the picture below.

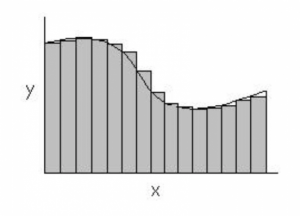
As the rectangles get narrower, the approximation of the area will be more precise, but keep in mind that it is still not the factual area, because we will always have either underestimate or overestimate value, depending on which point (the left point or the right point of the rectangle width) was chosen to make the calculation. One aspect to consider is that when the curve gets more irregular the approximation of the area will be more difficult to calculate.

Just like the examples that show previously, integration could be applied widely no matter in real life or abstract math problems. In order to find the most efficient solution, based on the concept of simplification, we connect some scattered parts to form a valuable whole through a particular way, which is the main idea of integration.

Group members:
Clarissa Audrey 51844165
Mariana Paspuel 44069169
Violet Ye 52433166
Chelsea (Tong Cui) 31032162

About the Question 3 in this midterm , there are 3 parts need solving. Although the forms are different, fundamentally speaking ,they are all related to the definition of  continuity. So the key to solve this kind of problem is to understand what is the continuity.

continuity means “constancy “, let us think about what if a function is continuous in its domain , it should be complete, without break ;  it should be smooth, without jump.

Look back to Question 3, about (a) we use the definition of continuity to define g(x) to be continuous at a , and about (b) , we need  to define what it means for a function f(w) to be continuous at g(a), we can just represent g(a) as a certain number just like a, and now we can find it has the same form as the question (a) . About (c) , although the form looks more complicated than (a)(b), the key to solve the problem is also simplification, and we also use the knowledge about the definition of limit to combine g(x) with f(w) to get the answer.

About the Question 3 in this midterm , there are 3 parts need solving. Although the forms are different, fundamentally speaking ,they are all related to the definition of  continuity. So the key to solve this kind of problem is to understand what is the continuity.

continuity means “constancy “, let us think about what if a function is continuous in its domain , it should be complete, without break ;  it should be smooth, without jump.

And now give the real definition of continuity

A function f is continuous at x=a provided all three of the following are true:

(i) the function f is defined at a

(ii) the limit of f as x approaches a from the right-hand and left-hand limits exist and are equal, and

(iii) the limit of f as x approaches a is equal to f(a).

The function must satisfy all three requirements, if one of these is not fit, the function is not continuous.

Look back to Question 3, about (a) we use the definition of continuity to define g(x) to be continuous at a , and about (b) , we need  to define what it means for a function f(w) to be continuous at g(a), we can just represent g(a) as a certain number just like a, and now we can find it has the same form as the question (a) . About (c) , although the form looks more complicated than (a)(b), the key to solve the problem is also simplification, and we also use the knowledge about the definition of limit to combine g(x) with f(w) to get the answer.

If we want to understand the distinguish between convergent series and divergent series, we first need to understand what is a series, in the former web page about the convergent sequences and divergent sequences, do you remember the example I give about the baby ducks. We get a sequence{1,2,3,4,….} . And a series is the sum of every figures in a sequence. For the sequence {1,2,3,4,….}, its series is sum=1+2+3+4+5+…+n .

And now let us understand what is convergent series and divergent series by reading a famous story. According to the legend,  a mathematician invented the chess and he was awarded by the emperor , When he was asked what reward he would want, After thinking, the mathematician wanted to put one rice in the first check of the chess, then put two rice in the second check, put four rice in the third check, put eight rice in the fourth check…. And so on, the number of the rice in every check is twice as the rice in former check. The emperor agreed the mathematician’s asking and wondered why the  mathematician ask for so little reward. But soon the emperor was in a big surprise. The country did not have enough rice to fulfill all checks. Because when the 64th check was fulfilled, there were 18446744073709551615 rice. And if it continues, it will be bigger and without a limit.

And in mathematics, we can transfer the figures in to a series{2+2^2+2^3+2^4+….+2^n} and it is also the sum of every figure in the sequence{2^n}. From the story ,we know it is infinity and without a limit. So we can define the series as a divergent series.

From the story above, we know use limit to identify a divergent series. And in contrast, when a series has a limit or a scale to bound it, we can define it as a convergent series.

If we want to understand the distinguish between convergent sequences and divergent sequences, we need to understand what is a sequence, in mathematics, sequence is an ordered list of numbers. I know it is a little abstract. So let us think it into our real life.

When we go to the lakeside,  sometimes we can see a harmonious scene, a mother duck lead some baby ducks swimming in the lake. And they keep a line one by one. How can we know how many baby ducks in the line. May be we always count 1,2,3, 4…until the last baby duck. The number we have counted can write down as {1,2,3,4…} and this is a sequence. And in mathematics, the figures in a sequence can be different.

Another we need t know is about the limit. Limit is the most important difference between convergent sequences and divergent sequences. Generally speaking, a convergent sequence has a limit, and a divergent sequence has no limit.

Let us return to the real life. What is limit… When you are having a long-distance running, there is a time that you feel you can not insist  the running, the distance you have insisted is your running limit. And in winter,  we are considered with the temperature and predict whether it will snow or not. That is because, when temperature drop to 0 celsius degree zero，the raindrop will become snow and therefore 0 celsius degree is a limit.

Let us connect examples with mathematics. There is a classic example, if we have a stick and assume it is enough long,first we separate it into two equal parts. And then separate one part of the stick into two new parts…And repeat the behavior…Finally, we can find that this behavior can continue till forever and it will never have an end. So we can say it has no limit. And in mathematics, we can use the sequence {(1/2)^n} to represent the left part of the stick. And we define it as a divergent sequence.

The separation of a stick is a classic example to understand the meaning of the divergent sequence. We  know the divergent sequence has no limit. And in contrast，if a sequence has a limit and so we can think it is a convergent sequence.

Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!