All posts by Helen
Assignment 7 Examples
Group members:
Joe(Mu) Qiao 43042167
Tony(Qiyuan) Luo 44410165
Helen(Yuhao) Zhang 31019169
Integral examples
Please click on the file below
examples-integrals
The difference between “integration” and “antidifferentiation”
Students always think that integration is the same as antidifferentiation. Let us define these two terms now
Integration is a number associated with a function, what is usually called a “definite integral.” It is defined by a limiting process which means in a certain range or on a domain. That is what we have already learned, Riemann sum, in the class.
For “Riemann sums” by separate the domain equally into n rectangles and approximating the area under the function graph by adding those rectangles together, which are in the subinterval.
So, we can describe integration which is “definite integral” by this expression:
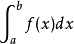
An antiderivative of f is a function whose derivative is f. Thus, if F is
an antiderivative of f, then F’= f. In another way, antidifferentiation is the reverse process of differentiation.
Antidifferentiation not focus on certain interval but work on the whole function. For example, f'(x) = 2x, then we know that the antiderivative of this function is f(x) = x^2.
We can define the antidifferentiation which is “indefinite integral” by this expression:
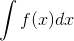
All in all, “Antidifferentiation” math circle is within “Integration” math circle. When we calculate integration we need to use the method of antidifferentiation.
Integration
From what we have learned we already know the method about finding the area of a square, a rectangle, a triangle, a circle and so on. We can apply the formula that works for each form which is related to get the area.
Right now if we want to find the area of any forms like a stain on clothes. There is no related formula for anomalous forms to find its area; however, we can transfer the form into those shapes that we already know.
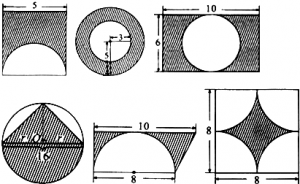
By using these known forms area we can get a similar area of an anomalous form. In order to get the value of the area more accurate to the actual anomalous form area, we can cut the area into as many known pieces as we want.
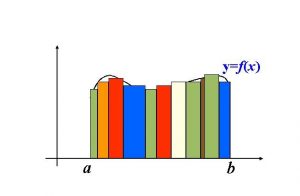like these rectangles
This method can also be used for finding the area under a curve. As the image shows below: 
To get the area closer to the real area, we can use more and more rectangle to separate the area under the curve, like the image below:
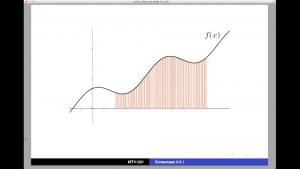
Joe Qiao 43042167
Tony Luo 44410165
Helen Zhang 31019169
“Secret” for unlocking the question in the test
The really important thing is before the test, you should handle all the statements that we learned in the class very well.
When you doing the test, first, read the question carefully, and find if there are some points or hints that directly relate to the knowledge that we learned before. Second, make sure the equation or idea that you get follow all the conditions that have been said in the statements. If not try to change the format or use other methods to get the solution. Third, once you get one solution check the answer make sure it follows what the question asks.
Also, suitable confidence helps a lot when you writing the test.
Comparing Convergency and Divergency In Sequences and Series
Convergent sequence has a real number as its limit, which means it sufficiently close to that real number. Like the picture below:
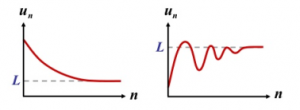
Let’s explain it by using some examples.
Ex.1
A sequence is an = {2, 2.01, 2.001, 2.0001, 2.00001, ……}. When n become as large as we want or we can say it arbitrary large, we will find that this sequence an is getting as close as we want or approach to 2. Since it is a real number, it means the sequence an is sufficiently close to 2, so an is a convergent sequence and it converges to 2.
Ex.2
A sequence is bn = {7, 8.5, 7.2, 8.3, 7.8, 8.1, 7.97, ……}. When n become arbitrary large, we will find that this sequence bn bounds and approach to 8 from above and below. Since it is a real number, it means the sequence bn is a convergent sequence and it converges to 8.
Here is the graph of divergent sequence:
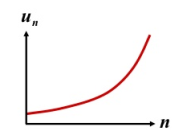
Divergent sequence does not have a real number as it’s limit, it just continue to get further and further apart which means away from 0 and any real number.
Ex.3
A sequence is cn = {1, 2, 3, 4, 5, 6, ……}. When n become arbitrary large, we will find that this sequence cn does not get close to any number. Since the limit is endless we can say it is infinity, it means the limit of the sequence cn does not exist, so cn is a divergent sequence.
Now let’s talk about series:
In mathematics, series is the sum of a sequence which contains n numbers. We use Σn≥1 to represent it.
Here is an image to show what are converge series and diverge series:
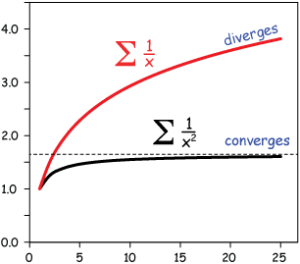
If we want a series which converges , the partial sums of its sequence has to have a real number as its limit, which means it sufficiently close to that real number.
Ex.4
A series is Σn≥1 ½n = {½ + ¼ + 1⁄8 + 1⁄16 + ……}. When the series add as many numbers as we want we will find that the number is REALLY small and the term become small very quickly. However, the series become large very slowly and getting close to 1. End up this series become sufficiently close to 1 which is a really number, so Σn≥1½n is a convergent series and it converges to 1.
If the series is divergent , the partial sums of its sequence does not have a real number as its limit, which means the limit of the series does not exist. The series just continue to get farther and farther apart away from real number,
Ex.5
A series is Σn≥1 1⁄n = {1+ ½ + ⅓ + 1⁄4 + 1⁄5 + ……}. When the series add as many numbers as we want we will find that the top values are equal or greater than the bottom ones, thus the sum becomes very large. End up this series does not close to any real number which means infinity and the limit of this series does not exist, so Σn≥1 1⁄n is a divergent series.
test
Hello world!
Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!