Category: mathFair

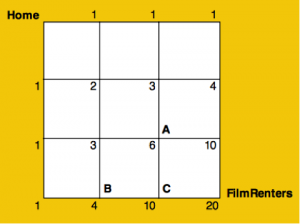
Problem:
1. How can you go straight to the FilmRenters from home when
there are buildings in the way?
2. Extension: How long is the shortest route from home to FilmRenters?

Children and their parents worked on the above stated problem at the Family Science and Mathematics Day at UBC.

We taped several copies of our statement of the problem at our station. As parents and their children walked past our station, some of them stopped to enquire about our problem. This problem was presented to our problem-solvers in several different ways. If a child were interested in the problem, we would state it as “how many different ways are there to go from this point to that point (pointing at the start and end points).” If both the parent(s) and their child were interested, we would pose the problem as, “how many different ways are there to go to your school from your home.” If the parent(s) were interested in the problem, we would pose it as “how many different ways are there to go to the grocery store from home with the shortest distance.”

Children started thinking about and engaging with the problem right away. Several students pointed out that their first solution was to go diagonally straight from the start to the finish. We entertained their first solution, just so that they would engage with the problem a little bit more. Then we slowly added constraints by asking, “what if there are buildings that you cannot go through” or “what if your parents/guardians are driving you.” Their parents were encouraging their children by often times saying, “oh yeah, that makes sense.” These constraints seemed to have caught some of them off-guard. For them, I guess that going through, over, or under seemed completely plausible. Even though the printout of the problem appeared to mimic 3-dimensional objects, I suspect that some of them might not have noticed this detail. One student even ran away to the physics lab when we introduced the constraints. With these constraints, I think that some of the children understood that this problem was related to day-to-day events of going from one place to another. Some of them were like, “oh, I get it. It’s like walking on the side of a road.” Once they understood the problem, some of them were reluctant to move on to other activities at the fair. They were glued to this problem.

This problem turned out to be surprisingly difficult for most of the problem-solvers. Once they understood the problem, they randomly started guessing, checking, and tracing different paths with their fingers. We even noticed one student moving just his head when tracing the path. Since they were randomly searching for and finding solutions, we asked several of them to simplify the original problem and start finding solutions with 1 x 1 block and then to move on to 2 x 2 blocks. This suggestion seemed to have worked a little bit. Many of them were able to find all the solutions to 1 x 1 and 2 x 2 blocks, however, without finding a pattern. This meant that when they moved onto the 3 x 3 blocks again, they were randomly looking for solutions. At this point, we gave another hint. The hint was to consider either the upper or lower half of the blocks along the diagonal. After spending more than half an hour at our station, this hint led to one child solving the problem completely. Her mother was separately working on the problem and didn’t seem to be surprised when her daughter was able to solve the problem. As the mother-daughter duo were about to leave our station, we asked them think about the case of 4 x 4 blocks and how it may be related to the Pascal’s triangle.

I think that we unintentionally made the process of solving our problem difficult. First, we did not provide any paper or pencil so that problem-solvers could somehow keep track of their solutions. Second, the printout of the statement of the problem was not of good quality. Third, the visual presentation of the problem itself was not appealing (no manipulatives). Last, some of the students appeared tired and were reluctantly directed to our station by their parents.

The presentation of this problem could have been improved. Instead of the A4 color printout, we could have actually created visually appealing graphics that would have looked like real roads and the building could have been pattern blocks (or some manipulatives) stacked together. Instead of tracing the paths with their fingers, we could have provided miniaturized cars, bikes, or something else so that problem-solvers would be able to visualize what it was that they were doing. Even better, use of 2-D and 3-D software to recreate this problem would have been much more appealing to many students, who appeared to be tech-savvy. By using technology, we could have eliminated the mundane (but sometimes useful) process of keeping track of previously found solutions.

This problem could be extended to the secondary level with minor changes to the constraints of the problem. For instance, we could ask students to create interesting variations to the original problem, come up with strategies to generalize the number of different paths for n x n blocks (or irregular shapes), or relate to prior knowledge from other areas of mathematics (polynomials, Pascal’s triangle, combinatorics, etc.).

If I had an opportunity to meet with some of the problem-solvers from this fair, it would have to be the mother and her daughter, who were intent on solving the problem. Often times, we incorrectly assume that teachers are the primary sources of fostering mathematical knowledge, curiosity, and problem-solving abilities. At this fair, I witnessed that the mother and her daughter were supporting and encouraging each other to solve the problem. From time to time, the mother would look over her shoulder and ask her daughter a question or two. Like, “wow, how did you get that many” or “can you show me how you did that.” To which the child would explain her reasoning behind her gradually increasing number of solutions. Their enthusiasm to solve the problem seemed to feed off each other’s ideas and interests. It appeared to me like it was more of an ongoing partnership or teamwork to solving problems than anything else. Over the course of working on the problem, the mother did say that she likes mathematics and that she likes to solve puzzles with her daughter in the evenings. It was encouraging to see how parental involvement at home and support at the fair led them to concentrate for an extended period of time to successfully solve this problem. So I can kind of understand why her mother was not too surprised by her daughter’s problem-solving abilities.

• Fourth Math Fair
• Third Math Fair
• Second Math Fair
• First Math Fair

Problem:
1. Shuffle a deck and place one card face down on a table.
2. Ask your child to turn the card over. If it’s a diamond, he gets to keep it. If it’s not a diamond, you get to keep it. Continue playing for 10 rounds and see who has the most cards after play has concluded.
3. Ask your child if the game is fair? Why or why not?
4. How can the game be made fairer?

K – 3 children from Trafalgar Elementary School worked on the above stated problem.

We ran into several issues right from the start. We were talking in a language that our students were unable to connect/relate to. I think that we were not using child appropriate language when describing and posing the problem. First, some of the terms, such as dealer, player, suits of a deck, round, fair, etc., appeared alien to many of the students in this context, even though a majority of the students knew how to play a game or two with a deck of playing cards. We repeatedly heard the phrase, “that’s not fair,” despite taking turns when dealing the cards, following the rules of the game, and winning regularly when dealing the cards.

Second, many students seemed to have a hard time trying to count (counting one card twice or not counting at all) the number of cards. This may be partly because the decks were slippery and the cards were too small for the children to handle. On several occasions, students ended up miscounting because of this.

Last, the decks were not sufficiently shuffled from time to time, which led to the player winning a game as opposed to the dealer winning the game. This happened with the first group of students. We didn’t elaborate why this was a possibility, because we thought that the students would not be able to understand the underlying concept of measuring fairness in probability and also due to lack of time. Indeed, when a player had won a game as opposed to the dealer (the dealer had a higher chance of winning a game) winning the game, we did not know how to explain what had just taken place to these students. In these instances, we ended up modifying the game in order to reduce further confusion. Instead of talking about fairness of the game or odds of winning or losing, we ended up steering away from these discussions. We asked students to come up with strategies so that no one would be able to win a game (indirectly bringing in fairness) if the whole deck was played. This modification created its own set of problems. For example, instead of playing a card game of some sort, some students ended up trying to divide the pack into two equal parts and then attempting to count the number of cards.

Winning or losing a card game appeared to be much more emotional to some students. A student who has won/lost the first round often guessed that he/she would win/lose the second round. I don’t know if this observation has any significance, but the body language of the losing player didn’t look too impressive until he/she won the next game. We also noticed that some students didn’t want to lose a game at all. When they did lose games, some students appeared visibly upset. Losing a game, regardless of whether they had won before, appeared to generate a broad range of emotions in some students that seemed to hinder full participation in follow-up activities. Some of them either threw their cards on the table, jump around, briefly walk away from the table, etc. This was noticeable especially when the new winner publicly displayed his/her emotions of winning by fist pumping or taunting the losing player. We tried our best to make sure that every student won or lost the same number of times before moving on to the second part of the problem.

Despite our best efforts to equally share students’ wins and losses, we noticed that a small number of students only wanted to win. These students not only wanted to win every game, but they also needed to win. Losing a game of cards seemed to visibly upset them.

I am sure that fairness is something that many students would have learnt or experienced in their daily experiences. Whether fairly sharing a pizza at home or things with others in their classrooms. In this particular context, it was hard to get some students to experience and understand how fair or unfair this game was. I am not sure if the gym played a role in bringing out the competitive nature of some of these kids. If I were to meet one of the student who said that, “that’s not fair,” I would want to get down to that child’s level of thinking and find out the reasons for this student to come to this conclusion. The game was definitely unfair to the player as opposed to the dealer. A follow up question would be to ask this student to come up with another game so that their game is fair. At his/her level of understanding, I think that this approach could also allow this student to engage with and experience the concept of fairness of games in general.

At the secondary level, this game could be used to analyze and investigate the probabilities of various outcomes. Secondary students would have prior experiences (flipping coins or card games) with the notion of fairness when it comes down to certain games or events. These experiences could be used to calculate probabilities, predict results, and develop algorithms or conjectures about experimental and theoretical probabilities when playing games like this one. Looking at probabilities through a theoretical lens will surprise many students, partly because many outcomes will seem to be counter-intuitive.

• Fourth Math Fair
• Third Math Fair
• Second Math Fair
• First Math Fair

Problem:
Students in Mrs. Como’s class are making up their own growing patterns. Angela uses triangle pattern blocks to make a growing fir tree.

1) Use pattern blocks to build and draw the next three fir trees in this pattern.
2) Predict what the tenth fir tree will look like and tell how many blocks you would need to build it.
3) Explain any pattern that you have used to find your solution.

Elementary school children from Henry Hudson Elementary School worked on the above stated problem.

As students arrived at our table, we handed out a piece of paper that contained the above problem. Then we requested them to read and follow the directions to solve the problem. A small section of students seemed to rush through the reading or not reading the problem at all. Instead, those appearing to be less interested in understanding the details of the problem just started making their own patterns using the blocks. Some of their patterns were very creative. In an ideal world, we would have encouraged them to look for some sort of repeating patterns within their invented patterns. But for the most part, students did spend a minute or two reading and/or re-reading the problem.

Many students used the triangle pattern blocks to start building models of the fir tree spontaneously. But several students appeared to have issues with understanding the problem after reading the statement of the problem. In these instances, either we rephrased the problem with the help of the pattern blocks or had one of their classmates rephrase the problem to their friend. When a student was explaining the problem to his/her friend, we noticed that the explainer had difficulties with verbally explaining the problem. So the explainer ended up using the pattern blocks to better understand and explain the problem to their friend. We also noticed blank stares with our explanations as well. I think that for some students, the triangle pattern blocks didn’t seem to look like fir trees. In these instances, we built several models of growing fir trees with them individually, and asked these students to continue to build the next fir tree separately, prior to searching for numerical representation of their patterns.

As students were in the act of building the fir tree models, we noticed that several students were constantly rotating their pre-built patterns. It was interesting to note that several of these students, who were rotating their pre-built patterns before building the next tree, ended up dismantling the whole tree structure. These students started from scratch to build the next fir tree, which meant that they were unable to keep track (but kept track of the total number of blocks used) of how the blocks were assembled to grow the fir tree methodically. Even though they kept track of the total number of blocks that were used at different stages, they appeared not to notice the pattern of increasing blocks by odd numbers. I think that these students were somewhat unable to connect with how their previous fir trees were built/assembled and how it may be related to the next tree. In turn, this may or may not provide further opportunities to notice different patterns or extend the problem in order to come up with alternative solutions.

Many students made some sort of a table to keep track of their growing patterns. What was surprising to us was that many of these students learnt to make tables a week or two ago in their math classes. So they brought their prior knowledge of making tables to organise information for this problem, which seemed to have made it easier for some students to notice the growing pattern. This strategy seemed to have worked for many students. Their written work, shown below, suggests this to be the case. Once they noticed a growing pattern from their table, often times, students guessed the next few steps and filled up the table. In order to verify that they had the correct numbers in their table of values, they built the fir tree and convinced themselves that they have indeed found the correct pattern. Not all the students were convinced about their predictions with respect to the number of blocks used to build the growing tree. As adults, I think that this is often the limitation of our understandings of mathematical proofs. We sometimes believe in a mathematical theorem/proof, but just want to check it with a random example or two to convince us that the theorem/proof, indeed, really works for arbitrary cases.

Once a pattern was found, we had a hard time to motivate the students to look for other patterns. This was not surprising. When we generally think of solving problems in mathematics, we often think of exercises in classes or homework containing just one solution. We can see from their written work that they have noticed the growing pattern in relation to consecutive odd natural numbers. I think that most of the students were just looking at one column, with the total number of blocks, rather than trying to find a relationship between the two columns. They may or may not have reached the point in which they would have learned to relate the two columns in a table. To my surprise, only one out of all these students went a step further and noticed the relationship between the two columns, and wrote his pattern in terms of the square of the natural numbers.

In fact, when we were deciding to pose this problem, we were not thinking about the growing pattern in relation to the odd consecutive natural numbers. I was not aware of this possibility and these students convinced me that they have a valid solution. All along, we wanted our problem solvers to notice another growing pattern in relation to the square of the natural numbers. The solution to the original problem did not mention about other possibilities and so we did not look for alternative solutions. However, we were receptive to other possibilities, but this may or may not be the case in their everyday classroom experiences when learning mathematics.

If I were to follow up with the student who noticed the relationship between the number of blocks used in the growing tree and the square of the natural numbers, I would want to know how he noticed the pattern. And perhaps challenge this student to tell me more about how he noticed the pattern, why he thinks his pattern is right, what’s next, or how might this problem be similar or different to something that he has encountered before.

This problem could be modified to cater to high school students. For example, one modification would be to ask students come up with patterns by counting the number of vertices or edges for the growing tree. This may lead students to notice that their patterns are related to the Pascal’s triangle, which in turn is related to combinatorics. Another interesting modification could be to extend this to graph theory, where students would color the vertices or edges and noticing patterns with the growing tree.

• Fourth Math Fair
• Third Math Fair
• Second Math Fair
• First Math Fair

Problem:
Take away any 5 straws (or sticks) and leave 6 triangles.

https://woodcraft.org.uk/sites/default/files/Match%20stick%20puzzles.pdf

We posed the above stated problem to the sixth, seventh, and eight grade students at Norma Rose Point School.

One of the strengths of the problem was that there were multiple solutions to the problem. There were also multiple approaches to solving the problem. In addition, this problem required no prior experience in problem-solving in order to find the solutions. In other words, this problem was accessible to a wide range of learners with minimal instructions. I think that this problem was also fairly easy to pose, both verbally and physically manipulating the straws/sticks. Because this problem was simple to pose both verbally and visually, I think that it was somewhat easier for language learners to understand the problem. As soon as we finished posing the problem, the majority of the students started looking for solutions. Right after posing the problem, students seemed to dive into rearranging the sticks.

There appeared to be a flow as students went about manipulating the sticks. The flow was temporarily interrupted by frequent shouts after finding solutions. Occasionally, these shouts appeared to distract some students from concentrating on what they were doing. Often times, some students walked over and looked at other students’ solutions. We were hoping for some sort of verbal interaction to occur between students who found a solution and those who went to look at a solution. For the most part, it was just a visual glance of the solution and nothing more than that.

In relation to language learners, this problem’s structure was decontextualized/simplified as much as possible (removal of extraneous information), almost appearing to be like a routine problem. Despite this, there were instances where language learners had difficulties understanding the stripped down version of the problem. In these cases, without our request for other students’ help, their classmates stepped in and assisted the students who could not understand the problem. In these instances, the assisting students appeared to translate our instructions both verbally and visually. After getting help from their classmates, language learners were able to successfully show/tell us (rephrase) that they have understood the problem and went about solving the problem, just like the other students.

One of the drawbacks about this problem was that it appeared to be a routine problem that was detached from real life situation. Nonetheless, this problem can be considered as non-routine partly because it had multiple entry points and numerous methods of finding valid solutions. Every student was able to find at least one solution and many other permutations of this solution.

The materials that were used to solve the problem both strengthened and weakened the approaches to finding solutions. We used different sized/colored plastic straws and two different types (small colored and large uncolored) of Popsicle sticks. One of the weaknesses of providing these manipulatives for solving the problem was that many students were quickly able to devise plans (not necessarily bad) to come up with valid solutions. That is, they were able to come up with strategies to solve the problem just by moving several sticks (after removing and holding on to five sticks), almost like their own algorithms. These strategies (sort of like looking for patterns or guess and check) produced only certain types of solutions (rotations of the same answer). Those students who employed these routines struggled to come up with different solutions. Many of the students, who were using these routines, were able to notice the rotational nature of the solutions, but couldn’t move beyond and appeared to get stuck. So these routines masked the possibilities of finding alternative solutions. Thus, some of the students were unable to devise alternative solution methods using these manipulatives.

I think that the majority of the students came up with multiple solutions on their own over the course of the mathematics fair. Although our intention was for students to work in pairs of two to arrive at solutions, it didn’t quite work out as planned for the most part. It appeared as if students preferred to work on their own, partly because we provided sufficient number of straws and Popsicle sticks. Even on instances when students started out in pairs, they quickly decided to work on their own. We noticed that group decision-making was hard for this problem. When thinking about our intentions, it was unreasonable to expect students to collaborate on moving a straw or a stick as a team. It was quicker to try multiple moves individually rather than making decisions as a team to make the moves. These students were too energetic and wanted to find the solutions. Despite many students preferring to work individually on this problem, many of these students not only shared their solutions with their peers, but they also explained about their methods of finding their solutions to us and to their friends.

Occasionally, we noticed one or two students talking to themselves about which straw or stick to move/remove. Some of these students were explicitly thinking aloud and explaining their reasoning to their peers, which I believe offered some sort of guidance to other students gathered around their table.

We made several modifications to our problem. Initially, we wanted to pose the following problem:

Take away any six matches (sticks/straws) to leave only three triangles

But we decided not to pose this problem as we thought that there was only one solution and one way of arriving at the solution. I think that our decision to not use this problem was partly based on targeting a wide range of problem solvers. Our objective was such that every problem solver would at least find one solution, if not all the solutions. We wanted every problem solver coming to our station to be a successful problem solver when they left our station. We were glad to have chosen a problem that enabled every problem solver to be successful at our station in the mathematics fair.

During the fair, we made several changes to the problem on the fly. We added additional constraints, such as each triangle should have no more than three sticks/straws. This constraint prevented the students from coming up with solutions that counted triangles (big ones) with more than three sticks/straws. We also discounted some solutions that had open-ended sticks/straws (i.e. when one end of the stick/straw was not touching another stick/straw.) I think that these changes enhanced the problem-solving strategies of some students and made the problem a little more interesting for others.

If we were to follow up with a student who claimed that she had found 14 solutions to our problem, we would have asked this student to show us one solution at a time and explain their thinking that this is indeed a solution. We would also challenge this student such that their solution might be rotation of another solution. The challenge would primarily be to create doubt in the mind of this problem solver so that this student really (re)think through the solution.

If we were to pose this problem to secondary students, it would probably be a precursor to a modified (but related) problem. In the modified problem, students would have to use logical reasoning to predict, generalize, and extend their understanding of the problem to other areas of mathematics. For example, going from solving a puzzle with physical manipulatives to finding abstract algebraic formulas. For instance, we could add another layer of triangles at the base (four more). We could then modify the problem such that when five sticks (or any predetermined number of sticks) are removed, then exploring how many different ways of finding a maximum or minimum number of remaining triangles. We could further complicate this modified problem by asking if there is a pattern in the minimum or maximum number of triangles as more layers of triangles are added to the base.

• Fourth Math Fair
• Third Math Fair
• Second Math Fair
• First Math Fair