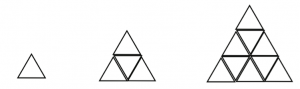
Problem:
Students in Mrs. Como’s class are making up their own growing patterns. Angela uses triangle pattern blocks to make a growing fir tree.
1) Use pattern blocks to build and draw the next three fir trees in this pattern.
2) Predict what the tenth fir tree will look like and tell how many blocks you would need to build it.
3) Explain any pattern that you have used to find your solution.
Elementary school children from Henry Hudson Elementary School worked on the above stated problem.
As students arrived at our table, we handed out a piece of paper that contained the above problem. Then we requested them to read and follow the directions to solve the problem. A small section of students seemed to rush through the reading or not reading the problem at all. Instead, those appearing to be less interested in understanding the details of the problem just started making their own patterns using the blocks. Some of their patterns were very creative. In an ideal world, we would have encouraged them to look for some sort of repeating patterns within their invented patterns. But for the most part, students did spend a minute or two reading and/or re-reading the problem.
Many students used the triangle pattern blocks to start building models of the fir tree spontaneously. But several students appeared to have issues with understanding the problem after reading the statement of the problem. In these instances, either we rephrased the problem with the help of the pattern blocks or had one of their classmates rephrase the problem to their friend. When a student was explaining the problem to his/her friend, we noticed that the explainer had difficulties with verbally explaining the problem. So the explainer ended up using the pattern blocks to better understand and explain the problem to their friend. We also noticed blank stares with our explanations as well. I think that for some students, the triangle pattern blocks didn’t seem to look like fir trees. In these instances, we built several models of growing fir trees with them individually, and asked these students to continue to build the next fir tree separately, prior to searching for numerical representation of their patterns.
As students were in the act of building the fir tree models, we noticed that several students were constantly rotating their pre-built patterns. It was interesting to note that several of these students, who were rotating their pre-built patterns before building the next tree, ended up dismantling the whole tree structure. These students started from scratch to build the next fir tree, which meant that they were unable to keep track (but kept track of the total number of blocks used) of how the blocks were assembled to grow the fir tree methodically. Even though they kept track of the total number of blocks that were used at different stages, they appeared not to notice the pattern of increasing blocks by odd numbers. I think that these students were somewhat unable to connect with how their previous fir trees were built/assembled and how it may be related to the next tree. In turn, this may or may not provide further opportunities to notice different patterns or extend the problem in order to come up with alternative solutions.
Many students made some sort of a table to keep track of their growing patterns. What was surprising to us was that many of these students learnt to make tables a week or two ago in their math classes. So they brought their prior knowledge of making tables to organise information for this problem, which seemed to have made it easier for some students to notice the growing pattern. This strategy seemed to have worked for many students. Their written work, shown below, suggests this to be the case. Once they noticed a growing pattern from their table, often times, students guessed the next few steps and filled up the table. In order to verify that they had the correct numbers in their table of values, they built the fir tree and convinced themselves that they have indeed found the correct pattern. Not all the students were convinced about their predictions with respect to the number of blocks used to build the growing tree. As adults, I think that this is often the limitation of our understandings of mathematical proofs. We sometimes believe in a mathematical theorem/proof, but just want to check it with a random example or two to convince us that the theorem/proof, indeed, really works for arbitrary cases.
Once a pattern was found, we had a hard time to motivate the students to look for other patterns. This was not surprising. When we generally think of solving problems in mathematics, we often think of exercises in classes or homework containing just one solution. We can see from their written work that they have noticed the growing pattern in relation to consecutive odd natural numbers. I think that most of the students were just looking at one column, with the total number of blocks, rather than trying to find a relationship between the two columns. They may or may not have reached the point in which they would have learned to relate the two columns in a table. To my surprise, only one out of all these students went a step further and noticed the relationship between the two columns, and wrote his pattern in terms of the square of the natural numbers.
In fact, when we were deciding to pose this problem, we were not thinking about the growing pattern in relation to the odd consecutive natural numbers. I was not aware of this possibility and these students convinced me that they have a valid solution. All along, we wanted our problem solvers to notice another growing pattern in relation to the square of the natural numbers. The solution to the original problem did not mention about other possibilities and so we did not look for alternative solutions. However, we were receptive to other possibilities, but this may or may not be the case in their everyday classroom experiences when learning mathematics.
If I were to follow up with the student who noticed the relationship between the number of blocks used in the growing tree and the square of the natural numbers, I would want to know how he noticed the pattern. And perhaps challenge this student to tell me more about how he noticed the pattern, why he thinks his pattern is right, what’s next, or how might this problem be similar or different to something that he has encountered before.
This problem could be modified to cater to high school students. For example, one modification would be to ask students come up with patterns by counting the number of vertices or edges for the growing tree. This may lead students to notice that their patterns are related to the Pascal’s triangle, which in turn is related to combinatorics. Another interesting modification could be to extend this to graph theory, where students would color the vertices or edges and noticing patterns with the growing tree.