Alphonse 47168166

Yuqi Liu 44616167

Chenming Hu 17973165

Qiwei Liang 33196163

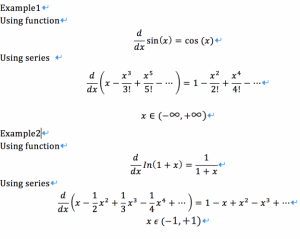
Integration: Integration is a kind of operation which calculates the area between the curve and x-axis in a given range. To integrate, we basically need a function and two x values which is the range of integration. Without these elements, it’s hard to do the integration.

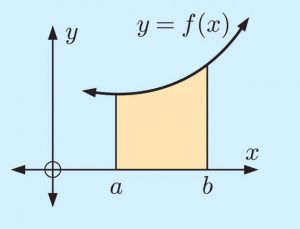figure 1

Take figure1 as an example, the integration of this graph is the yellow area. The formula of this area is abf(x)dx , as the formula shows,we need a value for a, b and the function of f(x). The integration will get an exact value of the area. When we integrate the function, the constant c does not matter in the formula. The result of formula will use F(b)-F(a) where F(x) is the anti differentiation of f(x). When F(b) minus F(a), the constant c will cancel out. We can also think about it by thinking about the graph. Adding c means the graph of anti differentiation function will increase by c. F(b) and F(a) will both increase by c. The difference will not change.

Anti differentiation: The process of solving for antiderivatives is called anti differentiation and its opposite operation is called differentiation. We assume that F(x)’=f(x), thus, f(x)dx=F(x). However, that is not true because it is incomplete. As we can see it clearly in this illustration,

when we get an f(x), and do the antidifferentiation for f(x), we can find a lot of function satisfy this equation; as the diagram illustrates, we can sketch countless curve with the same slope at every same point. So we can summarize that if we do the antidifferentiation for f(x), we can get an assemble of new function recorded by F(x)+C, C is a real number. For instance, given a function such as f(x)=x^2, do the antidifferentiation, then we can get the original function 1/3*x3+C.

Differences: The major difference between “integration” and “anti differentiation” is that the result of integration is a number, but the result of anti differentiation is an assemble of function, that means

when we want to do the integration, anti differentiation is a necessary step of it. As we introduced before, integration is the area of f(x) in a given interval, but in the diagram of F(x)+C, it illustrate the change value of F(x) in the given interval. However, we can easily find that no matter what the value of C, the change value in the given interval is always the same, because of the same slope all the time of F(x)+C. As the example before, f(x)=x^2, first we do the anti differentiation for it, we get F(x)+C, if we want the integration in [-1,1], we substitute -1 and 1 to the function, we get F(1)+C-F(-1)-C, no matter what the value of C, the result can be all the same.

Why confused:Why students always confuse about integration and anti differentiation?

It’s easy to mix these two operations together because these two operations will operation the original function in the same way. When students calculate about the function, they will look at the function and just calculate the value, they don’t think about what’s the operation, integration or anti differentiation. Obviously, the result is different. However, the process will confuse. Integration should calculate about the anti differentiation F(x) to get F(a) and F(b). Anti differentiation will get the similar result of the second step of integration, only difference by c. I think that’s the reason why students always confuse about these two operations.

Yuqi Liu 44616167

Alphonse Wang 47168166

Chenming Hu 17973165

Qiwei Liang 33195453

a) using the definition of the continue, the definition of limit.
b) using the definition of the continue, the definition of limit.
c) using the definition of the limit, and use the result from question (a) and question (b). Because g(x) is the basic function which has a relationship with x directly, and f(g(x)) is a function about g(x), so we should use g(x) to find the relationship between f(g(x)) and x, so firstly we using the definition of limit find out the relationship between g(x) and x, and figure out the epsilon and delta, and then using the definition of limit again, find the new epsilon and new delta of f(g(x)), and compare two epsilons and two deltas, and find out the result.

a) what distinguishes convergent sequence from divergent sequences
When n is approaching to the infinity, the convergent sequence is close to a real number not approaching to the infinity. For example, the sequence {1/n}, in this sequence, when n is approaching to the infinity, 1/n is approaching to 0.
When n is approaching to the infinity, the divergent sequences do not approach to any real number or approach to the infinity, For example 1) {(-1)^n}, in this sequence, we cannot figure out what is the data when n is approaching to the infinity, it can be 1 or -1. 2) {n^2}, in this sequence, when n is approaching to the infinity, the sequence is approaching to the infinity as well.

b) what distinguishes convergent series from divergent series.
Convergent series is the sum of the sequence is close to a number. From the ratio rule, when the |r|< 1 in a series, this series is convergent. For example, the series{1/(n^2)} Divergent series is the sum of the sequence is close to the infinity. From the ratio rule, when the |r|> 1 is a series, this series is divergent. For example, the series {2^n}.

Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!