Author Archives: xinquan zhu
Questions about the taylor series

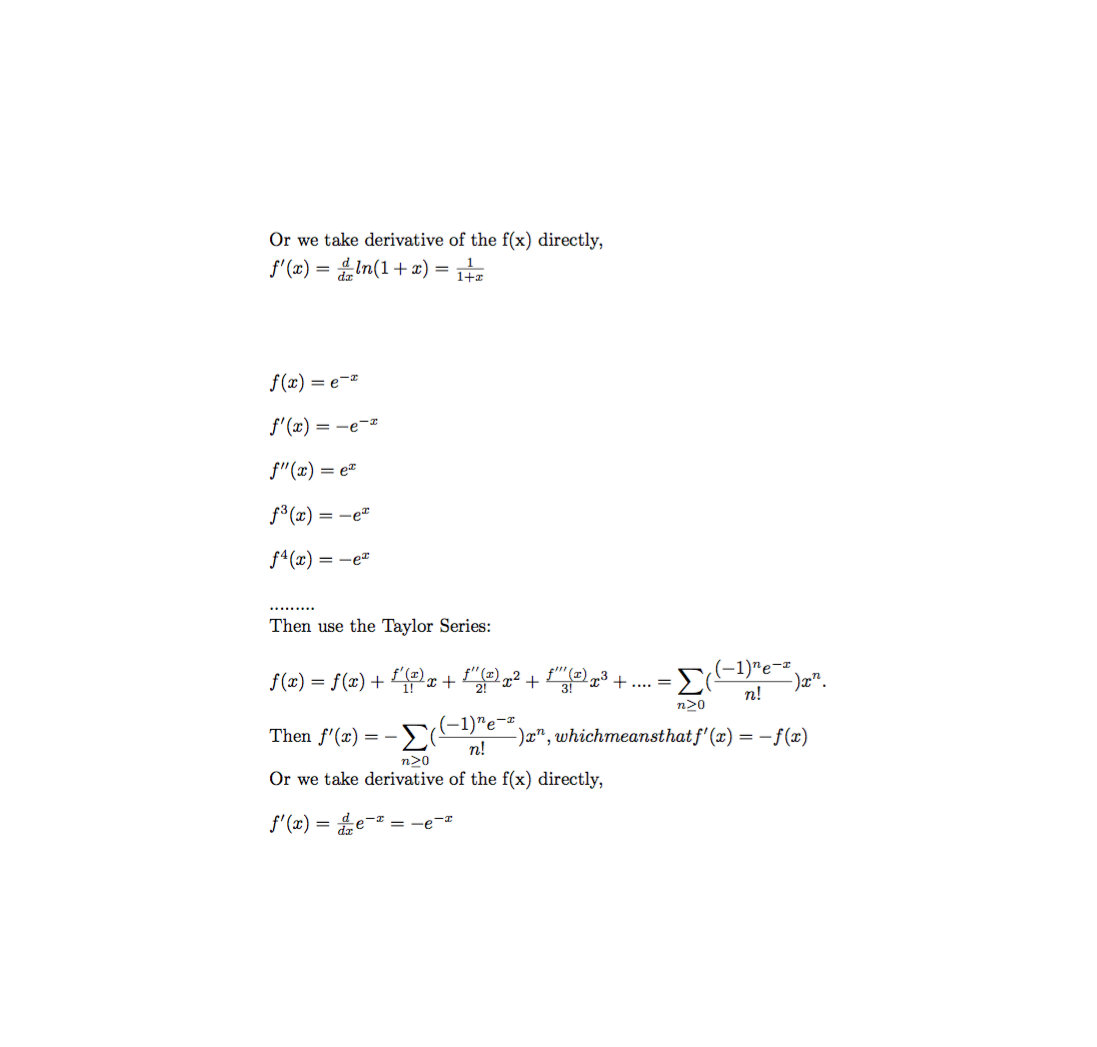
3 questions that used 2 kinds of integral calculation method
untitled (5) (pdf.file)
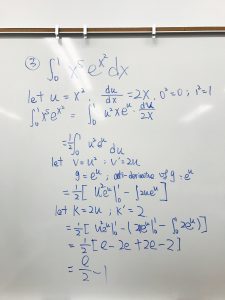

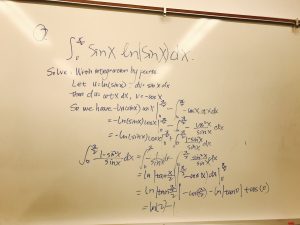
Here’s the question&solution code for overleaf user:
\documentclass{article}
\usepackage[utf8]{inputenc}
\begin{document}
\bigskip
1. calculate $\displaystyle\int_0^1 x^5e^{x^2}dx$
\bigskip
Let $u=x^2$, $\frac{du}{dx}=2x$, $0^2=0$, and $1^2=1$
\bigskip
$\displaystyle\int_0^1 x^5e^{x^2}dx=\displaystyle\int_0^1 u^2xe^u\frac{du}{2x}=\frac{1}{2}\displaystyle\int_0^1 u^2e^udu$
\bigskip
Let $v=u^2, v’=2u, g=e^u$, and anti-derivative of $g=e^u$, then the function will be $\frac{1}{2}[u^2e^u\big|_0^1-\displaystyle\int_0^1 2ue^u]$
\bigskip
Let $k=2u,k’=2$, then the function will be $\frac{1}{2}[e-2e+2e-2]=\frac{e}{2}-1$
\bigskip
\bigskip
2.calculate $\int_{0}^{3} (2x^3+18x)sin(x^2+9)dx$
\bigskip
$=\int_{0}^{3} 2x(x^2+9)sin(x^2+9)dx$
\bigskip
According to substitution method
\bigskip
let $w=x^2+9, dw=2x$
\bigskip
$=\int_{9}^{18} w\cdot sin(w)dw$
\bigskip
According to integration by part method
\bigskip
let $u=w, du=dw, v’= sin(w)dw, v=-cos(w)$
\bigskip
$= -cos(w)w|_9^{18}- \int_{9}^{18} -cos(w)dw$
\bigskip
$= -cos(w)w|_9^{18} +sin(w)|_9^{18}$
\bigskip
$=sin(18)-sin(9)-18cos(18)+9cos(9)$
\bigskip
\bigskip
3. calculate $\displaystyle\int_0^{\frac{\pi}{2}}sinx lnsinx dx$
Solve: With integration by parts. Let u=$lnsinx$, $dv=sinxdx$
\bigskip
Then $du=cotxdx$, $v=-cosx$
\bigskip
So we have that $-ln(sinx)cosx|_0^{\frac{\pi}{2}}-\displaystyle\int_0^{\frac{\pi}{2}}(-cosxcotxdx)$=$-ln(sinx)cosx|_0^{\frac{\pi}{2}}$-$\displaystyle\int_0^{\frac{\pi}{2}}\frac{1-sin^{2}x}{sinx}dx$
\bigskip
$\displaystyle\int_0^{\frac{\pi}{2}}\frac{1-sin^{2}x}{sinx}dx$=$\displaystyle\int_0^{\frac{\pi}{2}}\frac{1}{sinx}$-$\displaystyle\int_0^{\frac{\pi}{2}}\frac{sin^{2}x}{sinx}$=$ln|tan\frac{\pi}{4}|-cos\frac{\pi}{2}-ln|tan0|+cos0$
\bigskip
=$ln(2)$-1
\end{document}
The Differences between integral and Anti-derivation
Definition of antiderivative:
Antiderivative is the inverse operation of derivative and is related to definite integrals through the first fundamental theorem of calculus. Given a function f(x), the antiderivative of that function can be F(x), which means F’(x)=f(x). It is the process to reverse the differentiation.
In math, a continuous function can have lots of antiderivatives. Therefore, we prefer to call a group of antiderivatives instead of a single antiderivative. G(x)=F(x)+c. We say G(x) and F(X) ARE both the antiderivatives of function f(x).
Definition of integrals:
Integration has a defined limit which It can be used to find areas and volumes with intervals. For the function f(x). The form , where c is a constant number. Here, the symbol means indefinite integral, function f(x) can be a integration with the constant number c. Usually, dx and the integral sign need to be used at the same time as a pair. It means the function f(x) is integrated with respect to x. The sign dx also tells people where the integrating function ends. If we change the variable x to t, the integrating function needs to end with dt.
We have learned fundamental theorem in class. In the first part of the theorem, the indefinite integral has close connection with antiderivative. If the function is continuous, we can guarantee the existence of the antiderivative of the function f(x). In the second part of the theorem, we can calculate the initial function f(x) by the given of any f’(x). If F(t) which is the anti-derivative of f(t) was given, then we can know the integral of f(x) on the interval [r,l]. However, if the integral is indefinite integral, we need to add a constant number C after the anti-derivative F(x) since any two antiderivatives differ by that constant.
But we actually know that antiderivative and integration are two different things in total, as we know, integral is a kind of area, if you don’t give me a number, but just an interval, I could give you an exact number, however, if I say that you give me the same function, but no exact numbers like “x=1”,”x=2”or something like this, it is impossible for me to give an exact number to you; On the other hand, the definition of these two things are different, antiderivative is the function before the derivative, but the integration is just an area that 1 or 2 functions can form; And actually, it is not rarely to think that there two concepts are two different things, like you cannot compare banana and plane, antiderivative is more like that, I have a program that coded in Dr.racket, I ran it, if without a real number, the program could not run forever, but actually if I input a number, then my codes will tell me that , “All Test Passed”, and on the other hand, integration is more like, how high the tower is, how much sand you’ll spend on it, the concepts are different from the beginning; And the other character that shows these two things are different is that, integral has an interval, but antiderivative don’t, because you’ll need the interval to calculate the value of the function; The second thing is that, we’ll never put an exact number into the function body that used for integral , but the definition of antiderivative shows that, we’re not sure that if there’s a “c” inside the initial function.

The “Motivation” section for the topic of “Integration”
“Integration” is an efficient way to find areas of all shapes. In our life, integration is often utilized to calculate the areas of irregular shapes with divisions of regular shapes. —————our group
In daily life, there exist lots of irregular shapes which the areas cannot be calculated directly. While the regular figures are much easier to find out, such as squares and rectangles. The irregular shapes are required to divide into small regular shapes. Each small regular shape has the same size and shape. In this way, area of each small shape can be calculated. Eventually, we are able to obtain the area of the irregular shape which is approximate the sum of all small regular shapes.
For an example, we’ve played a game called “angry bird”, this should be an interesting game that could analyze the relationship and integration in a different way. As we know, there exists a slingshot on one side on the field. And we all know that there should have a string on the slingshot. The thing is, when you tend to pull the string with a greater starter energy, the bird will have greater energy, and this could also make more damage to the squares and pigs, we know that, if we accumulate little energy on the bird, the bird can just fly across the distance that is just a stone’s far away. Similarly, the “damage” which is made by birds is a kind of accumulate of energy, when the energy is big enough, we can see the effect clearly, this effect is what we call “integration”. This is just an unformal analyzation, in order to sufficiently give kind of definition of the word “integration”, we can also use an example about cake to analyze it, which can explain integration easily and clearly. Pancake is one of the most common breakfasts in our real life. And it is hard to measure the irregular shape of pancake. What should we do if we want to know the area of the pancake? One way that can measure the pancake is using square(s)! If we use only one square to measure the pancake, we will get the most inaccurate result. However, if we use countless squares, our result will sufficiently close to the correct result. The more squares we use; the more accurate result we have. That is the key of integration.
In conclusion, integration is important because it can be applied to determine the area of the irregular shape, which is hard to determine or to get the exact value by calculation. The basic idea of integration is dividing the irregular shape into some shape that are small enough but easy to determine and adding those regular shape together to get the value of the irregular shape. In addition, integration is one of the keys content of Calculus.
Divergent and Convergent
Sequence and Series
A sequence is like a box that full of balls, and the number of the balls are all different, pick some balls from the box, and they are now moved into a brand-new box, if we let all these balls in some special order, then balls in the box could be a sequence. And the ball which have many balls inside should be the series.
Divergent and Convergent of the sequence:
Maybe we can imagine the convergent of the sequence as take out money from your debit card, and you’re the richest man all around the world, but if you do not save money into your card but keep take money from the card, so there must have a time when you taken all the money from the card (but you still have the card, and it still has its value, so it means you might not going to be a bachelor);
Divergent of the sequence is like saving money to the bank, and there are more and more money in your card.
Divergent and C convergent of the series:
We can think about the series like the velocity of saving money, maybe the velocity of saving money is going down, but you’re still saving money, so there are more and more money you’ll save, this is diverge.
We can think about the velocity of taking out the money is going down, so there should be a limit that you can not take out any money from the card because the velocity is 0, but you still have money in your card, this is converge.
Hello world!
Welcome to UBC Blogs. This is your first post. Edit or delete it, then start blogging!