Explore constructivist TELEs

for math and science

As an investment analyst focusing on educational technology start-ups with math and business undergraduate backgrounds and a junior student in the MET program, I did find this course challenging from time to time. My surface knowledge regarding pedagogies and the lack of on-field teaching experiences limited my ability to share my thoughts and practices with the class. On the other side, I believed I could be one of the most enlightened students in this class since I achieved rapid absolute growth, from a low starting point. Throughout my learning journey in ETEC533, the course benefited me not only by assigned course readings and listed TELE projects, but also through intensive class discussions and mandatory reflections. The dynamic manners of this course design and implementation enabled me to explore various constructivist technology-enhanced learning environments(TELEs) with curiosities and engaged me effectively to participate in a respectful and vibrant learning community.

In the development of my learning trajectory, I found a clear path to understand the purpose and importance of why and what we are designing for the future with several key categories. They are: my interests, constructivist PCK and TPCK, traditional TELEs and emerging TELEs.

My Interests

My job as an investment analyst for the education technology industry offers me a wide range of flexibility to explore based on personal interests. Unlike most of the students in ETEC533, I don’t teach either math or science, and my curiosity flows across all subjects. Thus, I particularly appreciated the first module and initial lessons of this course to remind me the personal and specific meaning of education and technologies for myself.

My early memory regarding using digital technology was in Grade 5. That was the first time I used the search engine to find the answer to a tricky Olympiad math problem in grade 5. In the Auto e-Ograph discussion of a well-remembered event, I wrote down: “I was amazed by the search engine’s prompt and accurate response, then I realized I could utilize the internet to solve all kinds of academic problems! It was in 2003 and it was a magical night to me”. After I shared my first impression with educational technology with the class, I realized the wonders and beliefs of technologies in math learning took place deep inside my heart like deeply imbedded rocks. My selection of occupation also seemed to be an echo of my own unexpressed thoughts and natural feelings.

Since I was born in 1992 and had my first computer lessons in Grade 5, I often consider myself a digital native. Instead of using computers for learning, since Grade 5 and before work, I used computers for entertainment purposes most of the time. Similar to many of my peers at that age, I was addicted to different games during my spare time, including but not limited to family computer (FC) games, computer games, mobile games, video games on various game consoles(PS, XBOX, Wii, Switch…). From my experience, I knew how powerful digital games could be utilized for educational purposes for digital natives. In terms of engaging and fun for young learners, no other methodologies can compare to digital games. Therefore, in my next post, without referring to any books or resources, I proposed from my perspective “the good use of technology in learning math and science could be leveraged to solve math and science classrooms’ most challenging problem: the learning engagement” (Week 2 Discussion: Unpacking Assumptions). Based on my observations, I believed “the variety of educational technologies would offer less-engaged students with practical tools to visualize concepts, fun opportunities to explore related topics of personal interests, and empowered channels for interactive learning”.

Based on the progressive learning and discussions during the first three weeks, I re-framed my exploring topic to “how to effectively use Game-Based Learning (GBL) to promote learning engagement in math” for assignment 1. For this annotated bibliography assignment, I chose to analyze three high-quality scholarly articles, and two of these papers were meta-analyses written in recent years.

1. Based on an experiment participated by 25 students from a public secondary school in the Southern United States, Moon and Ke (2020) corroborated my underlying assumptions of “Game-Based Learning (GBL) can effectively promote learning engagement”, as well as “learning engagement can foster the development of mathematical thinking”.
2. The second paper from Abdul and Felicia (2015) scrutinized major gaming elements that help learners to attain high learning engagement. The study samples 91 peer-reviewed journals supported with empirical evidence. Then authors suggested practical strategies for designing a meaningful game-based learning environment according to their findings,
   “the learning experience is considered more sensory and playful if the learning content is accessible through a selection of virtual characters, environments, narratives, and multimedia elements. These elements are integrated to facilitate attention and to promote the player’s interest, which in turns triggers his/her engagement, providing opportunities to observe and browse visuals but not to read.”
3. The third analysis from Chen, Shih and Law (2020) revealed that digital game-based learning (DGBL) had produced improvements for learning outcomes. Through well-structured quantitative analyses based on 25 articles written in the past 10 years, this research demonstrated that competition in DGBL was effective for math, science and language, but not for social science and other subjects. It was effective for K-12 students and college students. It was effective for puzzle, strategy, role-playing, and simulation, but not for action games. Finally, competition in DGBL was equally effective for cognitive and non-cognitive engagements.

To summarize this annotated bibliography, I concluded, “although my choice of journal articles all have limitations in that they were conducted with relatively small samples within a unique context, there is a lot to be learned that may inform a wider audience. These studies provided insight into current perceptions and learning needs of 21st-century students; insights that could be useful in informing teacher practices of gamification, GBL, digital GBL, serious play in mathematics to address my question: how to use GBL to promote learning engagement in math effectively.”

Constructivist PCK and TPACK

The artifact from 17 Innovative Mathematics Projects that Inspire Students.

I resonated with Shulman’s statement of how a knowledgeable teacher that knows general pedagogical strategies can not be a good teacher (1986). At that stage of learning, I wrote, “unlike the tons of scientific simulation experiments with and without technologies, there is a lack of entertaining or comprehensive programs designed for secondary math classrooms”(Week 6 Discussion: PCK & TPACK), which later was proven to be completely false. As one of the classmates Allan Carmichael recommended in the various following course forums, Geogebra and Desmos are great websites for math simulations. These two sites and apps are designed with an intuitive user interface to play around on variables and their corresponding 2D/3D graphs. For that post, I also shared some PCK constructive activities for math and believed one of those artifacts (as shown above) was so gorgeous that the beauty and magic of this mathematical graph would inspire and engage all artistic students in learning math..

Traditional TELEs

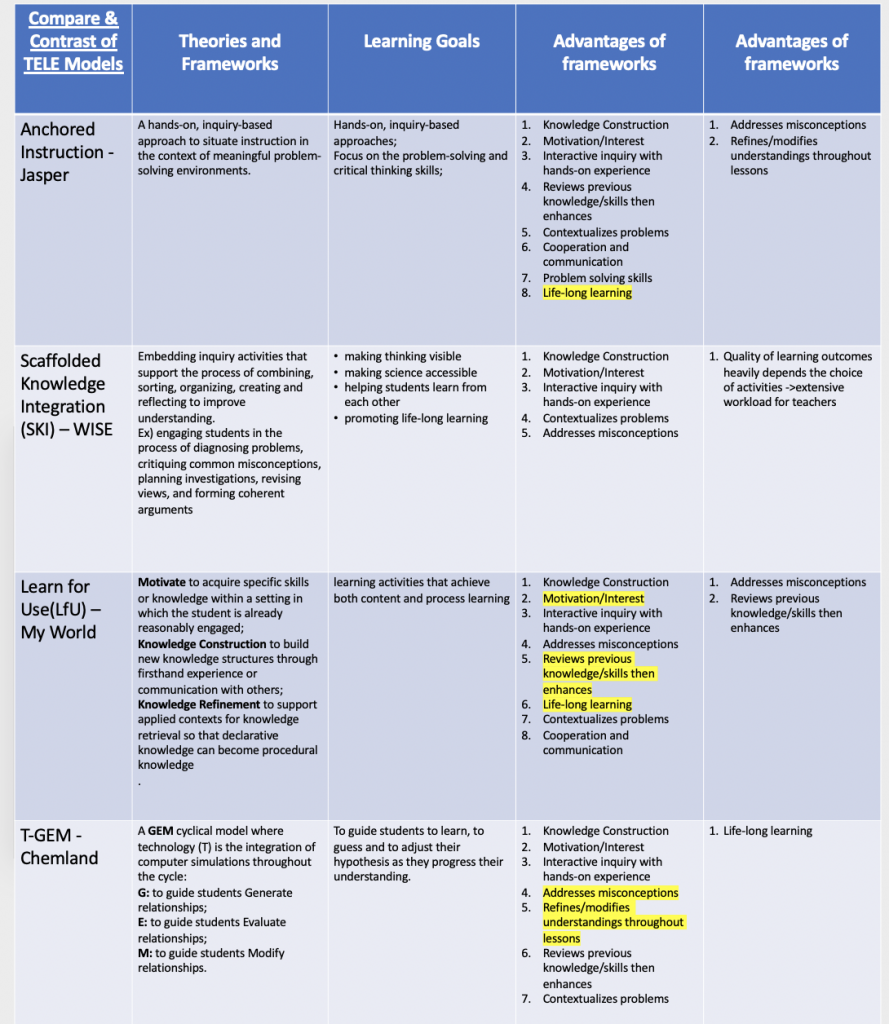
My synthesis of 4 frameworks and their applied TELEs

After a comparison and analysis of strengths and weaknesses of 4 designing frameworks and related projects, I wrote,”among the 4 cases provided by the course content, I particularly love the My World and related GIS projects since it provides a meaningful purpose for students to learn content knowledge. GIS-related projects could also develop life-long skills and promote life-long learning” (Week 10 Discussion: Synthesis Forum).

I was also excited to design my first lesson based on the TGEM model from Khan (2007) and Zhang et al.’s (2020) introductory to a tablet game, Motion Math. Motion Math is an interactive game for students in grade three to learn challenging concepts of rational numbers. The lesson design was simple, but I realize I missed the most critical elements of the curriculum form Halimat Alabi’s (the instructor) comment: how would I assign students for class activities. Do they work in pairs, or do they work individually? By thinking about these questions from Halimat, I realized the importance of social and interactive context among peers in the constructionism theory (Week 9 Discussion: T-GEM).

Emerging TELEs

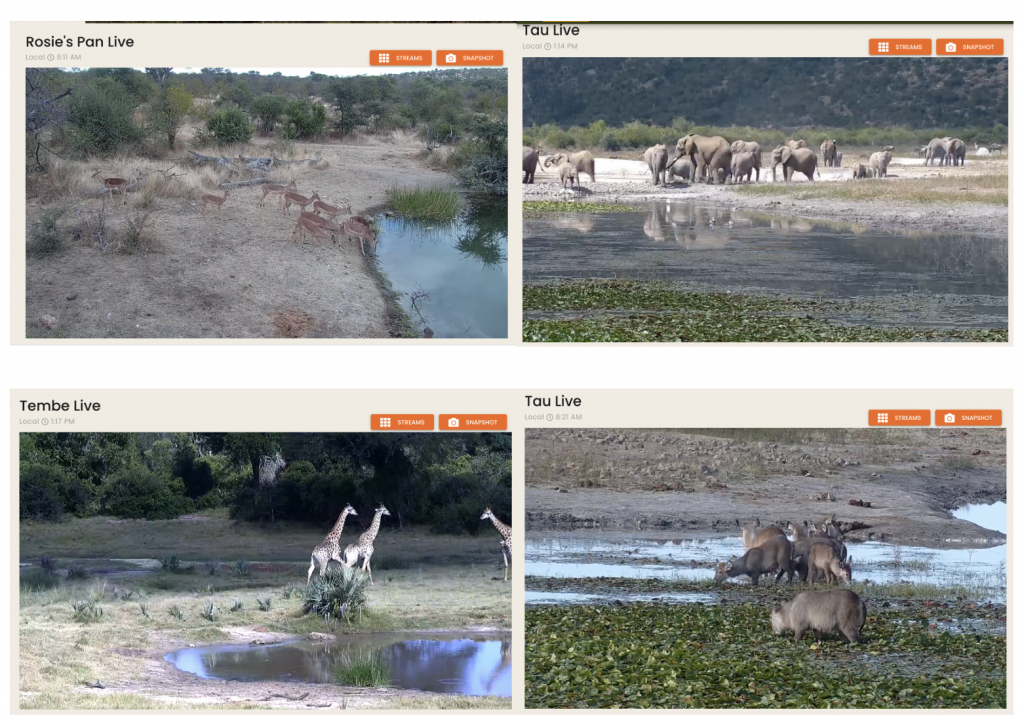
My screenshots of live streams from www.africam.com

As the most intriguing and recent category in this course, I dived into the world of emerging technologies and their applied projects. Two posts I shared in the weblog (Week 11 Discussion: Embodied Learning & Week 12 Discussion: Knowledge Diffusion) artificial environments and Smilevile, Virtual Field Trips and zipTrips™’ are only a tiny portion of available activities for free explorations (Abdul & Felicia, 2015; Adedokun et al., 2012). Sadly, in the year 2021, despite the extensive efforts by developers and educators in renowned institutions to design, adjust and promote these two projects, they both disappeared from the market.

Among other websites and TELEs I explored, I became a super fan of www.africam.com. I visited the website several times a day for recreational purposes in hopes of capturing live and idyllic moments of wildlife drinking, running, and sleeping across the African prairie.

Trying it all together

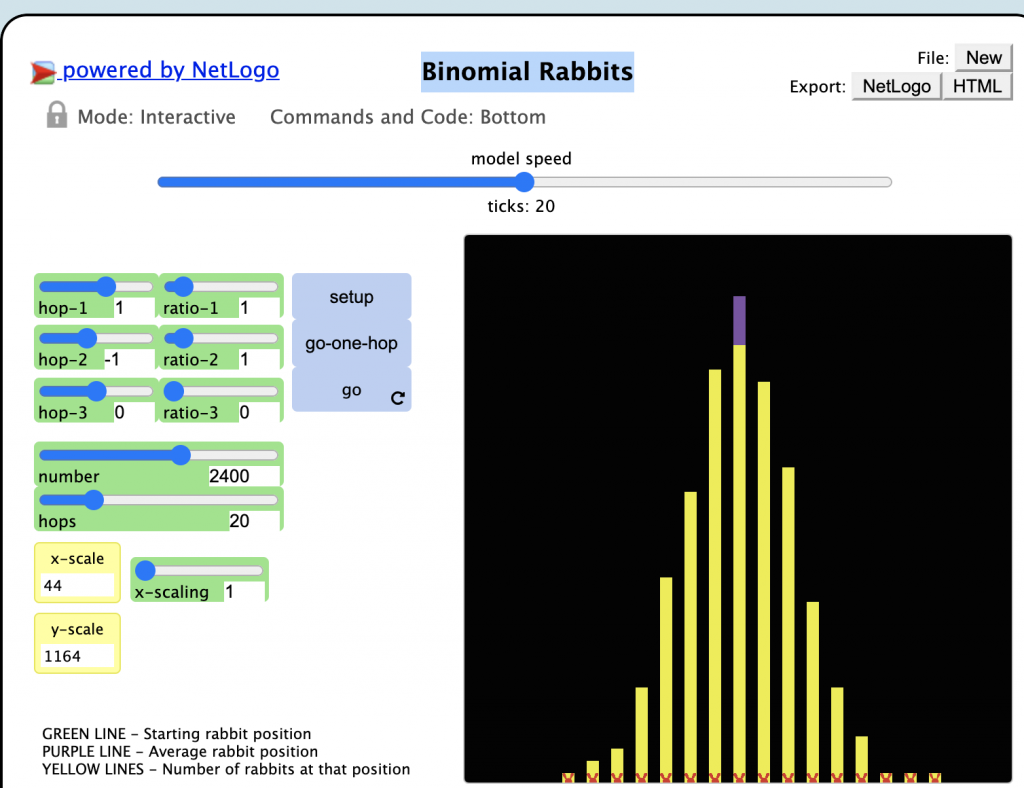
Netlogo simulation of Binomial Rabbits

For the Week 13 Discussion: Information Visualization, I tried designing a lesson for the second time of my life. I deployed the TGEM framework and Netlogo simulation of Binomial Rabbits to start the first Probabilities lesson in senior high school and introduce the normal distribution. The TGEM framework motivated students to learn detailed and complicated characteristics of the normal distribution by contextualizing the problem. Since the normal distribution is usually achieved through a vast sample pool, the Netlogo simulation enabled students to visualize the issue for an infinite large case.

With some improvements of adding the interactive context to the curriculum, I also found out my design missing the approximate length of time for each step after reading posts from other students. The length of time in a curriculum would provide teachers with a concrete plan of appropriate distribution for several activities and help teachers understand the plan’s emphasis.

Continued learning and designing opportunities

Updating a blog for a specific course is such a novel and meaningful learning experience to me. In the past, I had a folder for every class I had taken. These folders were built through four phrases: course overview and instructor’s information were added for preparation period, writing assignments, notes and other artifacts were accumulated throughout the entire course, then course readings were collected at the end of the course for possible uses in the future. Compared to weblogs, my traditional method has a limitation of prompt sharing. Simultaneously, the builds of individual weblogs will significantly benefit me as they provide learning spaces for reading posts from the past, current, and the future ETEC 533 students. As an addition, weblogs offer an open channel for peers to communicate and reconnect rather than the closed course space in LMS after the term ends.

Recent experience gives me the privilege of working with a team of developers interested in incorporating serious play into the course content. I believe all the readings I have done in ETEC533 would help me scrutinize every deployed pedagogies, designing frameworks, gaming elements, and delivery methods in our TELEs to promote intuitive thinking and active learning. And hopefully, this weblog and the other classmates’ weblog resources will be reviewed and utilized by my work partners and other students in the course of ETEC510, designing a TELE 🙂

At the same time, by learning and exploring TELEs, I will stay vigilant to the post-investment management of our currently invested companies’ TELEs at work. Both of the emerging TELEs I mainly explored in this course vanished from the market soon after the presence of projects, when there are still many academic papers on these two projects and appear in the course readings. The abandonments of TELEs seem to be normal even though they are educationally significant and proved with positive learning outcomes during initial trials. I will continue searching for some major reasons hidden behind these abandonments of TELEs and looking for corresponding solutions.

 

References and important course readings:

Abdul Jabbar, A. I., & Felicia, P. (2015). Gameplay engagement and learning in game-based learning: A systematic review. Review of Educational Research, 85(4), 740–779.
doi:10.3102/0034654315577210

Adamo-Villani, N. & Wilbur, R. (2007). An immersive game for k-5 math and science. Proceedings of the 11th International Conference Information Visualization, 921-924. http://ezproxy.library.ubc.ca/login?url=http://dx.doi.org/10.1109/IV.2007.23Links to an external site.

Adedokun, O. A., Hetzel, K., Parker, L. C., Loizzo, J., Burgess, W. D., & Paul Robinson, J. (2012). Using Virtual Field Trips to Connect Students with University Scientists: Core Elements and Evaluation of zipTrips™. Journal of Science Education and Technology, 21(5), 1-12. DOI 10.1007/s10956-011-9350-z

Alibali, M. W., & Nathan, M. J. (2012). Embodiment in mathematics teaching and learning: Evidence from learners’ and teachers’ gestures. Journal of the Learning Sciences, 21(2), 247-286. http://ezproxy.library.ubc.ca/login?url=http://dx.doi.org/ 10.1080/10508406.2011.611446

Chen, CH., Shih, CC., & Law, V. (2020). The effects of competition in digital game-based learning (DGBL): A meta-analysis. Educational Technology Research and Development, 68(4), 1855–1873. doi:10.1007/s11423-020-09794-1

Davis, B. (1997). Science teaching reconsidered: A handbook. National Academy Press. https://doi.org/10.17226/5287 (Links to an external site.)

Edelson, D.C. (2001). Learning-for-use: A framework for the design of technology-supported inquiry activities. Journal of Research in Science Teaching,38(3), 355-385. http://ezproxy.library.ubc.ca/login?url=http://dx.doi.org/ 10.1002/1098-2736(200103)38:3<355::aid-tea1010>3.0.CO;2-M

King, A., (1993). From Sage on the Stage to Guide on the Side, college Teaching, Vol 41, No. 1 (Winter, 1993). pp. 30-35. Retrieved from: http://www.jstor.org/stable/27558571?origin=JSTOR-pdf

Khan, S. (2007). Model-based inquiries in chemistry (Links to an
external site.) (Links to an external site.). Science Education, 91(6), 877-905.

Linn, M., Clark, D., & Slotta, J. (2003). Wise design for knowledge integration. Science Education, 87(4), 517-538. http://onlinelibrary.wiley.com/doi/10.1002/sce.10086/abstract
Mishra, P., & Koehler, M. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. The Teachers College Record, 108(6), 1017-1054. Text accessible from Google Scholar.

Moon, J., & Ke, F. (2020). In-game actions to promote game-based math learning engagement. Journal of Educational Computing Research, 58(4), 863–885. doi:10.1177/0735633119878611

Shulman, L.S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4 -14. Text available on Connect.

Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114. Full-text document retrieved on April 8, 2021, from: http://www.hitl.washington.edu/people/tfurness/courses/inde543/READINGS-03/WINN/winnpaper2.pdf

Zhang, L., Shang, J., Pelton, T., & Pelton, L. F. (2020). Supporting primary students’ learning of fraction conceptual knowledge through digital games. Journal of Computer Assisted Learning, 36(4), 540–548. https://doi.org/10.1111/jcal.12422 (Links to an external site.)