Kevin Milligan

I’m presenting today at a conference organized by the University of Calgary School of Public Policy. The conference is about the Canadian personal income tax, and my presentation is about the rate and bracket structure that determines how progressive the PIT system is. The papers from the conference will eventually be published, but for now I’m just posting my slides and my script for the presentation.

Here are my slides.

Below is the script for the presentation.

—

Script for Presentation at Calgary Tax Conference

April 16, 2015

INTRODUCTION

I’d like to get as many of you as I can interested in the progressivity of the income tax.

Many people care about the whole distribution of economic wellbeing.  Not just alleviating poverty at the bottom, but also inequality of economic outcomes between the middle and the top. They want the government to shape the distribution of income.  If you’re one of those people, I likely had you at ‘hello’.

Another set of people are worried about fairness of economic opportunities. Miles Corak argues that high inequality of incomes begets low intergenerational economic mobility. For these people, progressivity is good because it helps ensure fair opportunities for all.

Finally, a third set of people might not be interested in fiscal progressivity at all, arguing that fairness requires all citizens to be treated equally, with equal proportional fiscal impact.

If you’re in that third group, let me try to make a pitch to you as well.

We know that many elements of our fiscal system are regressive—like sales taxes, for example. If you want overall fiscal proportionality for bottom middle and top, you need a progressive income tax to counteract those other regressive elements.

So, to get overall fiscal proportionality, you need income tax progressivity.

CARTER

How should the income tax be structured to create some progressivity? Let’s start by looking at the Carter Commission report from the 1960s.

Carter is well known for its articulation of the comprehensive income tax base which tries to capture all forms of income and treat them equally–“a buck is a buck”.

Less well known is Carter’s design for a systematic approach to rates and brackets. This is important because the rates and brackets put in place in the 1972 reform–and lasting to today–look very similar to what Carter recommended.

Carter’s approach is based on a particular concept of ‘discretionary’ spending. Carter argued that what was non-discretionary depended on what others similar to you were doing.

This concept meant that someone making $90,000 who got an extra $10,000 in income would still have some element of ‘non-discretionary’ spending within that extra 10k. Maybe you had to buy a bigger house to keep up with the Joneses. The flaw in this reasoning, to my mind, is that the family benefits from that bigger house, whether they felt they had to spend the money or not.

Carter further argued that above 100k, all spending was discretionary.  Thus 100k threshold was argued to be the threshold for the top tax bracket since all spending was equally discretionary from that point onwards.

If you think this discretionary/non-discretionary framework is flawed—and I do—then the whole structure Carter created for rates and brackets collapses.

So, I don’t think we can use Carter’s system.

OPTIMAL TAXATION

Let’s move away from Carter and see if we can find any inspiration for the shape of income taxes in the economic theory of optimal income taxation.

For the first 25 years of the optimal income tax theory, from Mirrlees in 1971 until the mid-90s, policy makers found little useful in the theoretical developments. The optimal income taxes looked weird and looked like OHIO–zero at both ends and HI in the middle. It didn’t look like anything we had, or would want to have.

But in the late 1990s, work by Diamond, Piketty, and Saez revolutionized optimal income taxation by relating it to parameters we can estimate and observe. Here is what they developed.

The optimal tax formula tells us what the marginal tax rate should be at each level of wages. The essential tradeoff elucidated by the formula is between efficiency and revenue-raising.

In the formula, the LHS has the marginal tax rate for any given level of wages. Let’s imagine as an example, we’re talking about the marginal tax rate at $50K of income. So, what we’re talking about is what the tax rate should be for someone earning exactly $50K.

On the RHS, we can see the efficiency terms in the denominator. The bigger they are, the lower should be the tax rate.

First is the elasticity of labor supplying how much work effort is displaced by higher taxes. If taxes go higher, some of those people earning exactly $50K might decide to work a bit less.

Next is the wage rate and the number of people at exactly that level of wage. This tells us how much economic output is at risk of disappearing because of the higher tax rate.  If there are a lot of people at $50K we care more about the efficiency loss than if there are only a few people.

These are all in the denominator, so the bigger are these efficiency costs at any level of wages, the lower should be the tax rates for someone at that level of income.

In the numerator of the formula is a term showing us how many people are at or above this wage level. This tells us how much revenue we’ll get by raising the tax rate. If we raise the tax rate at $50K we get extra tax revenue not just from someone earning $50K, but from everyone earning $50K or higher.

The more people there are above the $50K point, the more revenue the tax increase will bring in. When a tax brings in more revenue all else equal, the formula says we should push that marginal tax rate higher.

So, the key trade-off here is between efficiency and revenue, and that is how I think we should discuss the setting of tax brackets and rates.

Three important and practical lessons for policy come out of the modern income tax theory.

First, there should be big transfers to those at the bottom, and they should be taxed back fairly sharply even if that requires high marginal rates.

Second, there should be progressivity between the middle and the top, and this progressivity should grow when top incomes grow more quickly than middle incomes.

Third, we can’t push these top rates too high without hitting the peak of the Laffer curve.  In the paper, I show data suggesting this peak is likely in the 60%-65% range, which means there is likely room for some modest increases at the top that will still raise revenue.

SIMULATIONS

To understand what out income tax looks like right now, and how it got to where it is, I present some simulations using my CTaCS tax calculator.

For these simulations, here’s what I do:

• Take 2011 income distribution from the SLID and CANSIM; inflate and deflate to dollars for the years from 1962-2015.

• Assume everyone is single; try with and without two kids. Trying to keep it simple; avoid the complexities of the Family Tax Cut.

• Only consider federal taxes and refundable tax credits—no spending side programs like UCCB or Family Allowance.

• Calculate average and marginal tax rates for federal taxes.

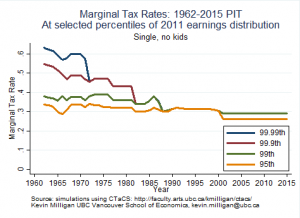
The first graph shows the evolution of the marginal tax rates for the highest earners. It shows the collapse of progressivity in the top one percent of the income distribution. In 1970, someone at the 99^th percentile faced a federal marginal tax rate of about 38%, whereas at the 99.99^th percentile it was about 60%. By 1982, that difference had collapsed to zero. So, our system no longer delivers any progressivity through the top of the income distribution.

The next graph shows the average tax rate across the income distribution for three different years, 1965, 1995, and 2015.

For 1965, taxes were zero for those at the bottom, then increased progressively until reaching those at the top, where the curve goes vertical, indicating a strong amount of progressivity.

For 1995, we see some negative average tax rates at the bottom. This is because of refundable tax credits, which are paid out even if no taxes are owing. From the 15^th to the 99^th percentile, 1995 taxes are just high everywhere, but do display some progressivity.

For 2015, there is a pronounced dip in the average tax rate for low earners, owing to the WITB. After that, the average tax rate is pretty close to the 1965 level until we reach the top 1%.

Now, let’s turn to what the system looks like today in 2015.

The next figure shows the marginal tax rate schedule for a family with two kids in 2015. The bumps and twists below $50K of income are generated by the WITB, the GST tax credit, and the regular tax brackets. Above $50K the CCTB is clawed back, and there is some progressivity in the rates.

When I look at this schedule, I wonder why so much of our thinking still revolves around the progressivity of the tax rates alone. The refundable tax credits clearly dominate the marginal tax rate schedule.

But, this isn’t necessarily a bad thing. Recall that the optimal income tax formula told us to tax back transfers quickly at high rates. The reason for this is the benefit of targeting; we save a lot of money by not paying the refundable tax credits for middle and higher income families.

Moreover, the efficiency costs of marginal tax rates for low earners are sometimes overstated. If workers care more about the ‘in or out’ decision than the marginal hours worked decision, then it is the average not the marginal tax rate we should care about. The chapter by Brewer Saez and Shephard in the Mirrlees Review gives a great overview of this ‘participation tax rate’ approach.

Finally, I show the ATR in 2015. It is sharply negative for many low earners. This pattern results from the refundable tax credits. For those of you who remember the old Family Allowance that paid $35 per month when canceled in 1992, let me tell you: this isn’t your mother’s baby bonus.

If I take the example of a single parent with two kids in BC, working full time full year at $12/hour, the graph shows the refundable tax credits she will get in 2015. This amounts to $662 per month, or about 32% of her wage income.  In addition to this, the family would get about $220 in UCCB, not included here. There is no WITB I this example because WITB is currently a very narrow tax measure that is fully clawed back at very modest incomes–so that it is completely gone even for a full year minimum wage worker.

To summarize what we’ve seen in the simulations:

• We have seen the complete elimination of progressivity within the top 1%, the income group that has seen by far the most income growth over this same time period.

• The rise of refundable tax credits has transformed the tax system for lower earners, especially those with kids. These tax credits have had a large impact on the incomes of those in the bottom quartile of the income distribution.

POLICY OPTIONS

To close my talk, I will go through four policy options that might push the income tax system toward more progressivity. I don’t necessarily recommend any of these options.  The goal here is just to assess what impact they might have on different parts of the income distribution.

I focus mostly on reforms that affect the middle and the top because the existing refundable tax credits have already pushed toward much greater progressivity at the bottom. There is a lot of room to consolidate these benefits to reduce complexity, of course.

These different options have different revenue implications. To get a very rough sense of magnitudes I take the Ready Reckoner from the Parliamentary Budget Office and add a dose of my known judgment.  The PBO numbers are meant for small marginal reforms, and some of my options are much bigger than that.

The first option is to increase the basic personal amount from $11327 to $20,000. This extends the ‘zero-rated’ tax bracket much higher, and would benefit everyone with income higher than the current $11,327 level. Since the credit is 15%, this amounts to a tax cut of about $1,300. The approximate cost would be $15 to $20B.

The impact is really large though most of the middle of the income distribution, but for higher earners it tapers out because $1300 doesn’t mean as much to their tax burden as it does to those at the bottom.

The second option is to increase tax rates at the top. For this example, I imposed new brackets of 35% at $250K and 40% at $400K. This reform gains revenue—it would result in a gain of $2 to $5B. By construction, this has no effect on low or middle earners. It does steepen the progressivity of tax burdens for higher earners.

The third example extends upward the tax bracket thresholds from $44,701 to $50K, from 89,401 to $100K, and from $138,586 to $250K. It would cost around $4 to $6B. It doesn’t have much visible impact, since the tax rate changes only in the overlap ranges between the old and new bracket structure.

Finally, I try lowering the rates in the two middle brackets to 18% and 22%. This would cost from $8 to $10B. It has an impact on median earners and higher.

CONCLUSION

My analysis began by trying to make the case for a progressive income tax, at the very least to counteract other regressive elements of the tax system.

I then argued that the Carter Commission’s bracket structure is hard to justify, yet the Carter structure was instrumental in eliminating progressivity among the highest earners.

Optimal income tax theory has become much more practical, and provides strong justification for progressivity between the middle and the top. The theory also provides support for the use of refundable tax credits at the bottom.

My simulations showed our tax system is doing pretty well at incorporating the refundable tax credits, but falling short on progressivity between the middle and top.

I offered some examples of reforms that could improve the progressivity between the middle and the top, finding very different pricetags on the different options.

I’m happy to hear feedback on this work and look forward to the comments by Dr. Sheikh.