What is infinity? I heard many different answers. A math student told me that infinity is the number with the greatest value, since infinity has larger value than any finite value, and it is great! In this post, I will give an introduction to infinity and present some of the interesting paradoxes of infinity.
Most people know infinity from the high school math courses. Infinity is just a result of a number divided by 0. The statements high school teachers taught are correct, but that is not the end for “infinity.” Infinity is a state or a concept. In the Oxford dictionary, infinity is defined as “the state of having no end or limit.” We know that infinity is greater than all other numbers, but what if we compare infinity with infinity? If there are two sets, each of which has infinitely many elements, which one is bigger and which one is smaller?
To answer those questions, let us start with how mathematicians compare the size of the set. To compare sets, mathematicians usually pair up elements, one from the first set and one from the second set. If each component can be paired with a component from the other set, and there is no element left after the pairing, they can conclude the size are the same. Consider the following scenario, we want to give candy to children, and we do not know how many candies are there. We can give one candy to each child. If we still have candy left after we give each child one candy, we know the number of candy we have is more than the number of children. If we run out of the candy before each child gets one candy, and some of them start to cry, you will know there is less candy than you expect (hope that will not happen).
Consider the following question, which set is larger, the set of odd numbers or set of even numbers? I think most of you will believe they have the same size. If you think this way, congratulations, you are correct! And consider this question, which set is greater, the set of natural numbers of the set of even numbers. I believe that most of you will believe the set of natural numbers is larger than the set of even numbers. Since the set of natural numbers are the set of odd numbers combining with the set of even numbers. However, they have the same size. Let’s verify the method we described above. We can try to match the even number with the natural numbers see if there are any numbers left after we match them. We can map two from the even number to the one in natural numbers, 4 to 2, 6 to 3,… In this way we can use the formula the even number 2n can map to natural number n to infinity, with no left elements from each set. The picture below also shows the idea.
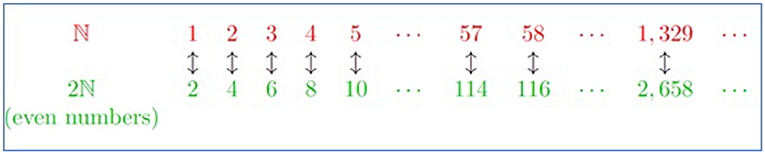
The picture shows the mapping from natural numbers to even numbers. From the article “Infinity and Trying To Do Maths With It”.
If you want to see some mind-boggling example of what happens if infinity happens in real life, see this video about Hilbert’s paradox of the infinite Hotel down below.
All the above examples I gave are only one kind of infinity. Mathematicians call it countably infinite. Countably infinite sets are the sets that we can pair each element in the set with a natural number, like even numbers, odd numbers, prime numbers and so on. But is that all kind of infinity? Does there exist other sizes of infinity? The answer is yes for both questions!

Picture from Wikipedia Cantor’s diagonal argument page
Consider a set of infinitely many strings with infinite length. For each pivot of the string, it is either 0 or 1. Then is this set countably infinite? Actually, the set is not countably infinite. This is proven by famous mathematician Georg Cantor in 1891, and his proof is known as the diagonalization argument. The idea is as follows: construct the following string, take the first element of the first string and flip it (if the original digit is 0, then take 1; if the original digit is 1 take 0) as the first element, and take the second element of the second string and flip it as the second element, and continue (show in the picture below). The constructed string is different from any string since it is at least one fliped digit that is different from any other string. So we created a string that we cannot assign natural numbers to. So the set is not countably infinite. A direct consequence is that the real number is uncountably infinite. This is a link to a formal proof of why real numbers are uncountably infinite using diagonalization argument.
http://mathonline.wikidot.com/the-set-of-real-numbers-is-uncountable
In fact, there is a more important consequence of the diagonalization argument. The power set of a set has greater size, even the set is infinite. The power set is a set of all the subsets. By this consequence, there are infinitely many uncountably infinite sets.
Although there isn’t much application to the size of infinity, they are the fundamental part of set theory, number theory, real analysis, and more. There are so many branches of mathematics that are built upon these abstract and fascinating ideas. Other than it’s importance in mathematics, it is also something really poetic about infinitely many sizes of infinity.
For a review of concepts of infinity, watch the video down below.
-(Sylvester) Shunkai Li
