When considering a challenging science concept, I recalled struggling with explaining the concept of floatation, or “sink or float”, when teaching kindergarten. Although exploring objects that sink and float in water is highly intriguing for young students, the reasoning behind which objects sink and float can get complicated and too abstract for a student at that age to fully understand. Why does a tiny popcorn kernel sink and a large watermelon float?
In the BC’s New Science Curriculum, density is not specifically addressed until grade six when students investigate heterogenous mixtures. In Suat Unal’s (2008) research, he recognizes that elementary students possess significant misconceptions relating to floatation as evidenced through other research by Biddulph and Osborne (1984) and Gürdal and Macaroglu (1997). This other research finds that “students offered many unrelated factors such as mass and weight” to explain floatation activity, and that even after sink and float investigations and learning of Archimedes had been completed, students “were unable to construct scientific understanding” about sink and float relations (p.135).
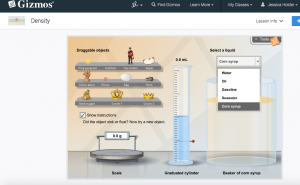
In preparing a T-GEM lesson, I wanted to include student investigation of objects that sink and float in water, as well as in other liquids, to help student understanding of the concept of density. Because of this specification, the Gizmos simulation that is included in the following lesson is ideal, whereas other simulations that I found online provide investigation solely with water. An image of the simulation follows:
T-GEM Lesson – Density – Grade 6 (BC Curriculum)
| Teaching Strategies | Student Activity | |
| Read Aloud – Chapter 5, “Archimedes and King Hiero’s Crown” from Archimedes and the Door of Science by Jeanne Bendick. | Class discussion narrating ideas presented through reading; teacher comments neutrally | |
|
GEM – Cycle 1 |
||
| G – Generate | Instruct students to investigate selected object in a sink and float investigation using water in a container. Students are to record observations on a T-chart as well as represent observations on a paper chart template using cut and paste images of the selected objects. Ask students to make a prediction about the types of objects that sink vs. float. | With a partner, students test sink and float tendencies of selected objects in water and record on a T-chart; Students place cut out pictures of objects onto chart template; After recording data, student journal predictions about the types of objects that sink vs. float. |
| E – Evaluate | Ask students to record anything that does not make sense about their observations and prediction – questions they may have or confusing patterns; Ask students to think of a way to conduct a sink and float investigation that could help clarify some of the observations and predictions that do not make sense. Prompt students with a change in variable – either the solid objects or the liquid. Teacher guides student through extension investigations using an alternate liquid. | Students discuss with partner and record observations and predictions that don’t makes sense; Share questions and confusing patterns with class and plan a new investigation with changing one variable. Watch teacher directed demonstration and participate in class discussion. |
| M- Modify | Ask students to determine what changes they need to add to their T-chart and paper pictorial chart to accommodate the new information accessed from the teacher-led investigation | Student makes adjustments to representations of t-chart and paper pictorial chart by including results with variable change. |
|
T-GEM – Cycle 2 |
||
| G- Generate | Direct students to Gizmos online simulations: https://www.explorelearning.com {Teacher needs to previously set up an account and select simulation to add to their “class”.}
Lead students to the the elementary level lesson under Physics called “Density” Provide a short explanation of the activity, sharing that instructions are provided in text within the simulation. Remind students to record on a new chart the weight (g) of the object when measured on the scale, the volume displacement (mL)of the object within the graduated cylinder, and the the ability of the object to sink and float in each of the available liquids (water, oil, gasoline, sea water and corn syrup). After all objects have been tested, journal a relation statement based on the acquired data. |
In partners, students use the Density simulation measuring weight and volume displacement of the following objects: ping pong ball, golf ball, toy soldier, apple, chess piece, penny, egg, rock, gold nugget, crown 1 and crown 2. Students will test the floatation of each object in five different liquids and record their observations. Students will analyze their data and make a relation statement in their journal. |
| E-Evaluate | Teacher provides students with the equation for density:
Density = Mass/Volume Water = 1.00 g/mL Oil = 0.92 g/mL Gasoline = 0.70 g/mL Sea Water = 1.03 g/mL Syrup = 1.33 g/mL |
Students compare the density of the measured objects using the density equation and with the density of the liquids and evaluate their relation statement making changes as necessary. |
| M-Modify | Ask students to design a pictorial representation (model) of the data. Students can choose to represent objects that sink, or float, or both. The model should include density measurements of both the liquids and objects. The model should include a comparison of two or more liquids. Recommend using a chart or graph format with pictorial representations of objects. | Students choose data to include in their model representation following criteria provided by teacher. |

Comment posted by Dr. Samia Khan
Hi Jessica,
Thank you for contributing a detailed T-GEM plan. It was informed by research on student conceptions such as, “students offered many unrelated factors such as mass and weight” to explain flotation. For your grade 6 class, you designed a TELE that involved a simulation and identified an affordance of this technology for your age group and curriculum: “I wanted to include student investigation of objects that sink and float in water, as well as in other liquids, to help student understanding of the concept of density.”
The T-GEM was a number of critical manouevers towards conceptual development. For example, reading, art, charts, scans, concept mapping, drawing, surveys, mini-quizzes are all ways to elicit prior ideas in math/science. Notable also in your plan is that teachers’ comments are neutral at the outset; there are no attempt to over-write student conceptions but rather to begin a process of questions to elicit how the grade 6 children think about this topic. The cyclical nature of GEM was also evident with 2 GEM cycles. This is an important component of GEM. (Sometimes the G is followed by E and M and then another cycle of E and M). There was also additional nuance: Direct teacher instruction can be a component of GEM as promoted by the chemistry teacher in the Khan studies (2007) and (2011) in this past week’s required readings.
A few ideas for elaboration: in the generation phase, it might be possible for students to ask each other questions based on their T charts, for example why did that object float float? In the Evaluation phase: given the selected objects, which ones are anticipated that won’t make sense to the students? Using anomalies in the way that I think you have developed is a potentially very powerful method. Clark Chinn writes more about this in his famous paper: Chinn, C. A., & Brewer, W. F. (1993). The role of anomalous data in knowledge acquisition: A theoretical framework and implications for science instruction. Review of educational research, 63(1), 1-49, and it was a method suggested in the case study an the Private Universe. In the Private Universe, when students suggest that the Earth is closer to the sun in summer as an explanation for the season, an anomalous piece of information is that the earth is actually closer to the Sun on Jan 04 than July 04.
It is worthwhile noting that there is an opportunity at multiple points for students to make a relation statement (in their journal). Making these relationship statements helps them to generate rules that can later be reconsidered, extended, or enriched beyond the case that they were originally applied to. These relationships may be qualitative, semi-quantitative (as X increases, Y decreases), or quantitative (equations, formulas).
In the modification phase, asking students to design a pictorial representation (model) of the data is one way to begin to inspect their conceptual understanding. it will be interesting to see how students represent heaver objects in these pictorial models. It would be very interesting to attempt to set the cycle up so that students are given the opportunity to come up with a relationship between mass, volume, and density before they are given the equation, as suggested by Darren and others. It would also serve to include the mathematics in the sciences or the science in the mathematics, consonant with STEM.
We look forward to hearing how your lesson went. Thank you, Samia