Tag Archives: Anchored Instruction

April 2, 2017 · 6:05 am

Financial Literacy for the Elementary Student – Coin Box Simulator Through Anchored Instruction

Background:

Financial literacy is highlighted throughout the elementary grade levels in the Content area of BC’s New Curriculum. Most paper-pencil curricula address money identification, counting coin and dollar amounts, and one or two step word problems connected to money. However, these paper-pencil activities minimally equip students for financial literacy skills and applications. While exploring the information visualization simulators during this past week, the elementary and middle school simulations from Illuminations were easy to understand and seemed quite plausible to implement into already developed curriculum.

Literature Support for Lesson Cornerstones: 

In a study conducted by Srinivasan, Pérez, Palmer, Brooks, Wilson and Fowler (2006), engineering freshman students who completed learning using MATLAB did not experience what they perceive as an authentic experience. The students felt that their experience was disconnected from real expert experience because they manipulated a simulated system rather than a real-life system. The researchers conclude that a probable reason for this disconnect is that the students “need/want authenticity to be able to make connections the experts make with the simulation” (Srinivasan, 2006, p.140).  This perception from the students leads educators to consider the value of real-life experiences in connection with simulated experiences.

Transferring simulated experiences to real-life experiences is supported through the study completed by Finkelstein, Adams, Keller, Kohl, Perkins, Podolefsky and Reid (2005). In their study, students in a second semester introductory physics course, who had used a simulation first to design a circuit system, were more successful later in designing real-life models. These same students also achieved greater success on related exam material that was completed two months after the simulated and real-life circuit building experience (Finkelstein, 2005). Due to these findings, authenticity of learning through the transferring of knowledge from simulation to real-life experience is a main cornerstone of the following lesson design.

In addition to authenticity, two lesser cornerstones, rich content and goal challenge motivation, are also incorporated into the lesson design as supported through the writings of Srinivasan et al. (2006). A pre-test assessment begins the lesson in order to determine prior knowledge and the optimal area of learning for the individual student. As well, this pre-test assessment can be used to determine pairings/groupings throughout the lesson activities. By providing rich content within the lesson plan, this affords opportunity for students with less prior knowledge to acquire new knowledge before exploring the simulated and real-life experiences. Building prior knowledge within students is critical for their success as Srinivasan et al. (2006) state, “Prior knowledge accounts for the largest amount of variance when predicting the likelihood of success with learning new material” (p.138). In regards to gaining knowledge of the student’s optimal area of learning, this connects closely to Vygotsky’s zone of proximal development, but is also supported by goal oriented motivation when learning goals are neither too steep, nor too simple: “If learning goals are too steep for a learner’s current context, learning is not successful. On the other hand, when learning is simple for the learner, the instruction can become over-designed and lead to diminished performance” (Srinivasan, 2006, p. 139).

Lesson Overview: 

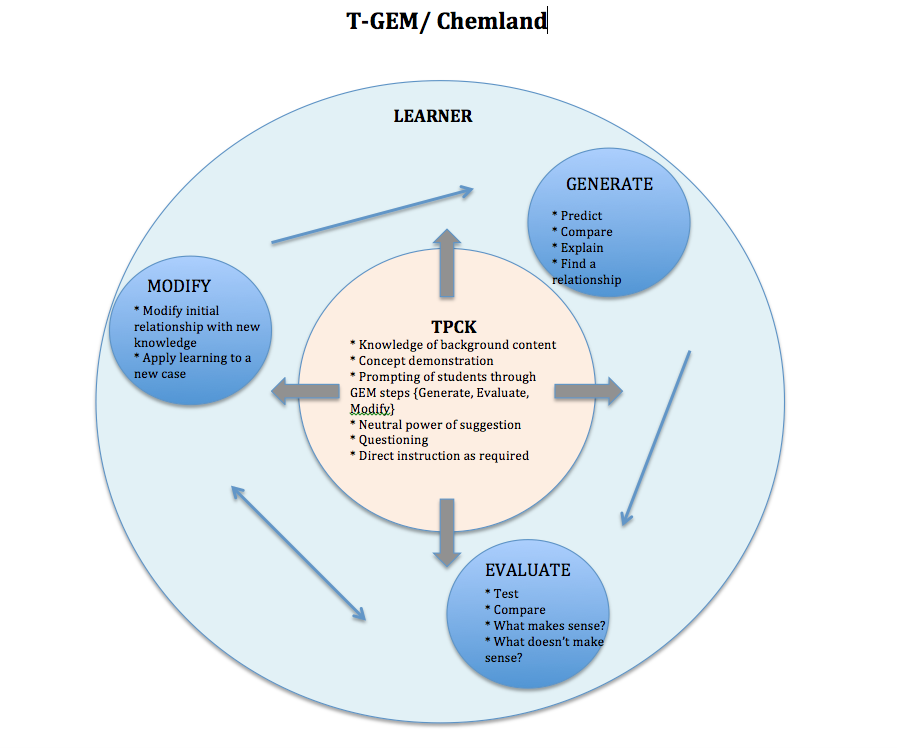
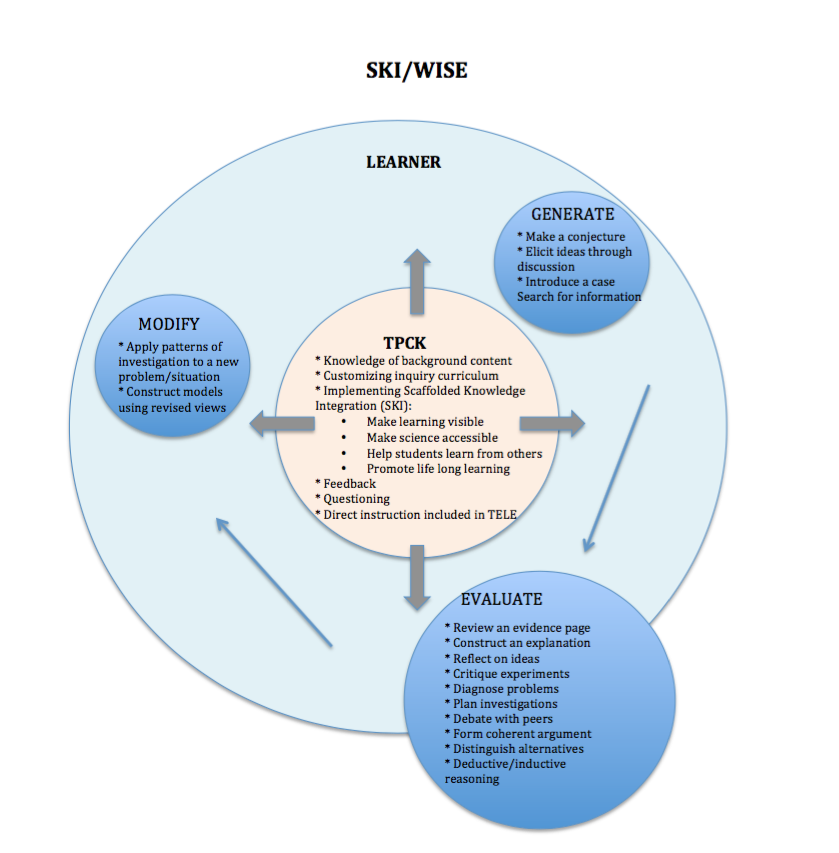
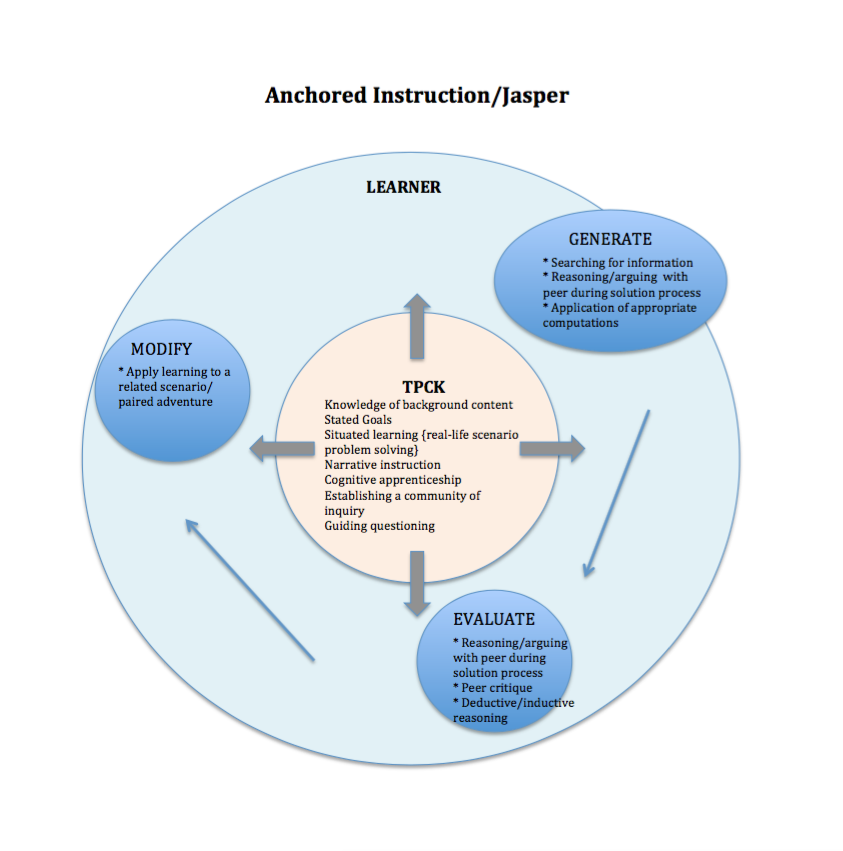
The following lesson incorporates the instructional framework of anchored instruction. This has been accomplished through a narrative multi-step problem solving feature. The three cornerstones highlighted in the section above are evident within the lesson: goal challenge motivation {decided by pre-test assessment}, content-rich material, and authenticity through real-life application.

LESSON

Pre-test Assessment:

Provide paper-pencil assessment including photos of Canadian coins asking students to identify individual coins.

Addition questions for pre-test assessment may include:

  • How many quarters makes a dollar? How many dimes? How many nickels?
  • Show 3 different ways of making one dollar using a mix of coin types. Draw coins with labelled amounts to share learning.

 Include two ‘making change’ questions that require student to calculate amount of change from $1.

Content-rich Material: 

Read and discuss Dave Ramsay’s book entitled, My Fantastic Fieldtrip on saving money.

Provide pairs of students with real sets of Canadian coins with accompanying anchored money solving problems. Problems may require students to interact with other students in the class or with the teacher. An example of an anchored money problem solving scenario follows:

Macey has been saving her allowance for seven weeks. She has a saving goal of $20.00. Each week she receives $1.50. Three weeks ago, Macey decided to buy her sister a rubber ball for her birthday which cost $1.00.  She used a loony from her savings . After seven weeks, Macey wanted to exchange all of her quarters for loonies, but she also wanted to keep half a dozen quarters for when she visited the candy machine at the grocery store when she went shopping with her mom.  She knew that several of her classmates had loonies that they could exchange for her quarters. (At this time, go around to your classmates and exchange your quarters for loonies just like Macey wanted to.) Once Macey exchanged her quarters for loonies with her classmates, how many loonies does Macey have? How much money does Macey have all together? How much more money will Macey need to save to reach her saving goal?

Simulation  Activity:

Illuminations –  Coin Box {elementary level}: Initially, direct instruction is required to demonstrate how by clicking on the cent icon in the bottom right corner, the student can see the amount of each coin as they are  US coins and difficult to decipher visually. Direct instruction should also be provided to guide the student to the “Instructions” tab and show the subtitled areas “Modes”. Student can then have time exploring the “Activity” section using the dropdown menu in the top left corner. Student should have ample time to explore all five activities including: “Count”, “Collect”, “Exchange”, “Change from Coins”, and “Change from Value”.

Transfer to ‘Real-Life’ Context: Students should have opportunity to transfer the simulated learning to a real-life context. An example of a real-life context is provided below, however adapting this to uniqueness of the learning community is recommended:

Cookie Sale –  Each student bakes one dozen cookies to sell to classmates and other students at the school. Pricing: 1 cookie = $0.40, 2 cookies = $0.75, 3 cookies = $1.00, 4 cookies = $1.25, 5 cookies = $1.45, 6 cookies = $1.70. This activity allows for assessment by the teacher through observation. Student’s accuracy and ease of providing change could be assessed using a simple checklist. Students should work in pairs  or small groups to help ensure that change to buyer is accurate.

Self Assessment/Reflection: A reflection activity is to be completed by each student. This activity requires the student to reflect on and share about growth and relevancy of learning. A self assessment printable is here:

Self Assessment

Finkelstein, N.D., Perkins, K.K., Adams, W., Kohl, P., Podolefsky, N., & Reid, S. (2005). When learning about the real world is better done virtually: A study of substituting computer simulations for laboratory equipment. Physics Education Research,1(1), 1-8.

Srinivasan, S., Pérez, L.C., Palmer, R.D., Brooks, D.W., Wilson, K., & Fowler, D. (2006). Reality versus simulation. Journal of Science Education and Technology, 15(2), 137-141. doi: 10.1007/sl0956-006-9007-5

1 Comment

Filed under Uncategorized

Tagged as , , , , , ,

March 27, 2017 · 6:07 am

Authentic Learning with Nature

Through the readings from this past week, I have explored a seemingly disjointed array of ideas. Following is a brief overview:

Carraher, Carraher and Schliemann (1985) present the effect of contextualized learning on mental math computation processes with street vendor children in Brazil; Falk and Storksdieck (2010) share results from their study on adult leisure science learning at the California Science Center in Los Angeles; Butler and MacGregor (2003) provide an in-depth explanatory overview of the GLOBE program designed to enable “authentic science learning, student-scientist partnership, and inquiry-based pedagogy into practice on an unprecedented scale” (p.17)! Although these three readings are diverse in study and purpose, one significant theme pronounced itself throughout: the theme of contextualized learning. Regardless of the age of learner, socio-economical position, or location on this great planet, contextualized learning offers authenticity of learning and effective growth in both content areas and competencies.

When considering authentic learning, I like to refer to Herrington and Kervin’s (2007) definition:

      The nine characteristics of authentic learning include:

  1.     Authentic context that reflects the way knowledge will be used in real life.
  2.     Authentic activities that reflect types of activities that are done in the real world over a sustained period of time.
  3.     Expert performance to observe tasks and access modelling.
  4.     Multiple Roles and Perspectives to provide an array of opinions and points of view.
  5.     Reflection to require students to reflect upon knowledge to help lead to solving problems, making predictions, hypothesizing and experimenting.
  6.     Collaboration to allow opportunities for students to work in pairs or in small groups.
  7.     Articulation to ensure that tasks are completed within a social context.
  8.     Coaching and Scaffolding by the teacher in the form of observing, modelling and providing resources, hints, reminders and feedback.
  9.     Integrated Authentic Assessment throughout learning experiences on a task that the student performs i.e. project rather than on separate task i.e. test.

     (Herrington & Kervin, 2007)

Although all of these characteristics of learning are not prominently practiced in the networked communities explored during this past week, many, if not all, can be emphasized through teacher design by incorporating a combination of non-technology based and network community activities.

The follow learning outline is designed using the network community called Journey North along with other on-going non-technology nature study activities. As an individual and an educator who advocates for regular nature study as a part of one’s life, the Journey North community peeked my interest as a very viable resource to integrate with already implemented nature study practices with students from grades K-4. I have chosen two projects at Journey North that could be easily implemented with my younger distance learning students. Following is a chart with resources and activities aligned with the authentic characteristics of learning as described by Herrington et al. (2007).


Butler, D.M., & MacGregor, I.D. (2003). GLOBE: Science and education. Journal of Geoscience Education, 51(1), 9-20.
Carraher, T. N., Carraher, D. W., & Schliemann, A. D. (1985). Mathematics in the streets and in schools. British journal of developmental psychology, 3(1), 21-29. 
Falk, J. & Storksdieck, M. (2010). Science learning in a leisure setting. Journal of Research in Science Teaching, 47(2), 194-212.
Herrington, J. & Kervin, L. (2007). Authentic Learning Supported by Technology: Ten suggestions and cases of integration in classrooms.  Educational Media International, 44 (3), 219-236. doi: 10.1080/09523980701491666

1 Comment

Filed under Knowledge Diffusion

Tagged as , , ,

March 21, 2017 · 10:56 am

TPCK and Learner Activity – A Synthesis of Four Foundational TELEs

Following is a collection of visual syntheses comparing and contrasting T-GEM/Chemland with the following technology-enhanced learning environments: Learning for Use (LfU)/My World, Scaffolded Knowledge Integration (SKI)/WISE, and Anchored Instruction/Jasper. The visual syntheses contain a focus on TPCK and learner activity with the guiding TELE being T-GEM/Chemland, and all other TELEs being compared and contrasted through alignment with the T-GEM/Chemland framework.

Each one of these TELEs is developed on inquiry instruction and learning, with T-GEM/Chemland consisting of specifically model-based inquiry. Each one of these TELEs promotes a community of inquiry with purposeful teacher-student and student-student interactions. To emphasize the non-linear processes of inquiry, each visual synthesis is designed in a circular format.

Unique to T-GEM is the cyclical progress that the learner takes moving through the steps of the learning theory. Arrows are placed in each TELE’s visual representation to elicit the learner’s movement in comparison to the T-GEM’s model.


As a general mathematics and science teacher for elementary grade levels, the process of exploring, analyzing and synthesizing  the four foundational TELEs presented in this course has been transformational in my development of TPCK. Initially, the importance of CK (Schulman, 1986), and my self-diagnosed lack of CK, was convicting as I tend towards growing in pedagogical ideas and creative ways of implementing them. To further this conviction, my understanding of inquiry processes and the intricate role that the teacher facilitates in conducting a community of inquiry began to become clearer throughout the readings and discussions of Module B. Skillful inquiry instruction requires a facilitator who is saturated in CK, being equipped to prepare, respond, question, prompt, and guide with carefully considered PK. At this time, I am challenged as an educator to begin with one brave adventure in mathematics using an anchored instructional approach, and another brave lesson in physical science using a T-GEM approach. I am certain that I will be generating, evaluating and modifying all along the way.  

 

Cognition and Technology Group at Vanderbilt (1992). The jasper experiment: An exploration of issues in learning and instructional design. Educational Technology Research and Development, (40), 1, pp.65-80

Edelson, D.C. (2001). Learning-for-use: A framework for the design of technology-supported inquiry activities. Journal of Research in Science Teaching,38(3), 355-385.

Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.

Linn, M. C., Clark, D. and Slotta, J. D. (2003), WISE design for knowledge integration . Sci. Ed., 87: 517–538. doi:10.1002/sce.10086

Shulman, L.S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4 -14.

Leave a Comment

Filed under SKI, T-GEM, WISE

Tagged as , , , , ,

February 14, 2017 · 12:18 pm

Thinking Out Loud – A Conversation on Anchored Instruction

Alongside the writing on The Jasper Series by Cognition and Technology Group at Vanderbilt (1992) , Shyu’s (2000) research on implementing video-based anchored instruction in Taiwan, and Vye, Goldman, Voss, Hmelo and Williams’ (1997) research on middle school students and college students working through The Big Splash, are considered in the following response.

**********

Anchored instruction is based on the theories of situated learning, cognitive apprenticeship and cooperative learning with the aim to enhance student problem-solving skills (Shyu, 2000). Anchored instruction largely involves generative learning. CTGV (1992) describes generative learning, by quoting Resnick and Resnick, as necessary for effective learning. Concepts and principles “have to be called upon over and over again as ways to link, interpret, and explain new information” (p.67). Anchored instruction situates “the instruction in meaningful problem-solving contexts that allow one to simulate in the classroom some of the advantages of apprenticeship learning (CTGV, 1992, p.67).  As well, anchored instruction focuses on cooperative learning which allows for the construction of ‘communities of inquiry’ – a space for students to grow understanding through discussion, explaining, and reasoning or argumentation (CTGV, 1992; Vye et al., 1997).

One of the important nuances of anchored instruction specifically evident in the research of Vye et al. (1997) is the effectiveness of thinking out loud. In their research, two experiments were completed, the first with individual students and the second with dyads or partner groupings. In both experiments, the students were asked to perform their thinking out loud. In the first experiment, the student did not participate in any dialogue with another student, instead verbalizing ideas in monologue style. In the second experiment, the students participated in reasoning, or arguments, to reach a solution, consisting of both agreements and disagreement. The success of problem-solving through reasoning in a dyad setting is attributed speculatively to the active expressing of ideas and thinking verbally, and the monitoring of reasoning and problem solving ideas by the partner. Furthermore, the data showing goal and argument linkages indicates that “goals tend to be followed by arguments and argumentation often leads to new goals” (p.472). Interestingly, the data related to the types of arguments indicated that 33% of the arguments were positive in agreement, while 67% were negative, or disagreements, both of which often lead to a new goal (Vye et al., 1997). Considering this thinking out loud aspect of anchored instruction is transformational for math instruction in general, as math problem solving traditionally is completed visually on paper, on a technology screen, or mentally – in silence.  One math resource by Sherry Parrish (2014) that I have recently acquired is entitled Number Talks: Helping Children Build Mental Math and Computation Strategies. Although digital technology is not a component of this K-5 curriculum {except for a CD-Rom with number talk sessions to instruct teachers on how to implement number talks), the physical act of talking, communicating ideas, reasoning and recognizing that there are many ways to solve a problem are premised throughout. A similar resource for grades 4-10 by Cathy Humphreys and Ruth Parker (2015) is entitled Making Number Talks Matter. Both of these resources do incorporate problem solving, but not in the same way as the video-based anchored instruction highlighted in the readings – problem solving is very much computational, rather than real-life scenarios and these math talk conversations and problem solving are dependent on access to previous knowledge, rather than generating knowledge through the problem solving. However, both math talks and anchored instruction do include ‘talking about math’, allowing for misconceptions to come to light and for students to better understand the why, when and how of mathematics. When a student is able to speak their understanding, that understanding becomes theirs to own, and becomes a tool through which they are now learning.

In closing, Vye et al. (1997) mention other problem solving enrichments that have been established by others. Following is a collected list of further inquiry readings. These readings are referenced on p.479.

Problem Solving Reading List

References

Cognition and Technology Group at Vanderbilt (1992). The jasper experiment: An exploration of issues in learning and instructional design. Educational Technology Research and Development, (40), 1, pp.65-80.

Humphries, C. & Parker, R. (2015). Making number talks matter: Developing mathematical practices and deepening understanding, grades 4-10. United States of America: Stenhouse Publishers.

Parrish, S. (2014). Number talks: Helping Children Build Mental Math and Computation Strategies. Sausalito, California: Math Solutions.

Shyu, H.-Y. C. (2000). Using video-based anchored instruction to enhance learning: Taiwan’s experience. British Journal of Educational Technology, 31: 57–69. doi:10.1111/1467-8535.00135

Vye, N., Goldman, S., Voss, J., Hmelo, C., Williams, S., & Cognition and Technology Group at Vanderbilt. (1997). Complex Mathematical Problem Solving by Individuals and Dyads. Cognition and Instruction, 15(4), 435-484. Retrieved from http://www.jstor.org/stable/3233775

Leave a Comment

Filed under Uncategorized

Tagged as , ,

February 13, 2017 · 7:35 am

Reshaping Instructional Design: A Tale of Jasper Series Inspiration

Upon initially exploring the video-based anchored instructional tool entitled The Jasper Woodbury Problem Solving Series, skepticism on the necessity and the effectiveness of this resource as an enhancer of student learning through problem solving presented itself: Couldn’t effective complex problem solving exist without the use of contrived video-based scenarios? Even after recognizing the intricate seven design features highlighted in the article by the Cognition and Technology Group at Vanderbilt (1992), the effectiveness of the Jasper series wasn’t convincing. It was only through the actual viewing of video samples from the series, as well as reading through a storyboard version in the Vye, Goldman, Voss, Hmelo and Williams study (1997) that the ingenuity of this anchored instructional design tool became pronounced. CTGV (1992) defines anchored instruction as situated learning that occurs in an “engaging, problem-rich environment that allow[s] sustained exploration by students and teachers” (p.65). The Jasper Series is a problem-rich environment as problem-solving is initiated with a proposed challenge, and the proposed challenge can only be solved through a minimum of fourteen steps, thus requiring a prolonged inquiry and exploration period. In order to solve the problems, the initial problem and the problems posed along the way, the student is required to find embedded clues, pose new problems, and seek alternative solutions (CTGV, 1992). The complexity of the problem solving within the problem solving is unfounded in traditional math curriculums, ensuring that the Jasper Series is an instructional design tool worthy of consideration.

Through the ETEC 533 discussion, one posting has inspired me to move forward with the learning acquired through the Jasper series related viewings and readings. Allison Kostiuk, an elementary teacher, began designing and writing complex problems reflecting realistic and relevant narrative for her students. Kostiuk chose to complete this type of narrative by “incorporating the names of … students throughout the problems, investigating daily issues that arise for … students, and further personalizing the problem by using pictures of… students encountering the problem” (Kostiuk, 2017). This idea of designing personalized problems for students resonates with me as the thought had previously crossed my mind while working through the readings and viewings on the Jasper Series. However, I had not taken time to act upon it. Although designing complex video-based instruction is not plausible at this time, a dramatized audio story or simple dramatic retelling could be viable in presenting students with many of the similar design features as evident through the Jasper Series. Incorporated design features would include video-based or audio-based formatting to increase motivation, narrative with realistic problems, generative formatting, embedded data design, and links across the curriculum (CTGV, 1992). A designed storytelling video-based problem solving scenario is planned to be shared with students at the beginning of this upcoming month. Once completed, it will be available within this posting.

Originally, my TELE design was founded on the concept of reciprocal interaction involving direct input from the student and reciprocal output from the technology. To read the definition of my initial TELE design, please visit here: Reciprocal Interaction: A TELE Design.  Through the readings, viewings, discussions, and considerations related to the Jasper Series, it has become evident that the video-based anchored learning does not fit my original TELE design. Within the Jasper Series, the technology was outputting information while the learner acted as a recipient, inputting information into the mind and then outputting learning into the surrounding environment to work towards solving problems. Following is an altered version of a reciprocal interaction design model with the option for the student to interact through input and output with the surroundings, rather than solely inputting back into the technology. Although the concept of reciprocal interaction continues to be an important feature in my TELE design, interaction with the surrounding environment is essential in bringing relevance to the learning as well as offering the opportunity for collaborative learning and reasoning.

 

Cognition and Technology Group at Vanderbilt (1992). The jasper experiment: An exploration of issues in learning and instructional design. Educational Technology Research and Development, (40), 1, pp.65-80.

 

Kostiuk, A. (2017, February 10). Problem solving with anchored instruction [Weblog message]. Retrieved from  https://blogs.ubc.ca/stem2017/2017/02/10/problem-solving-with-anchored-instruction/
Citation in text (Kostiuk, 2017)
Vye, N., Goldman, S., Voss, J., Hmelo, C., Williams, S., & Cognition and Technology Group at Vanderbilt. (1997). Complex mathematical problem solving by individuals and dyads. Cognition and Instruction, 15(4), 435-484. Retrieved from http://www.jstor.org/stable/3233775

Leave a Comment

Filed under Uncategorized

Tagged as , ,