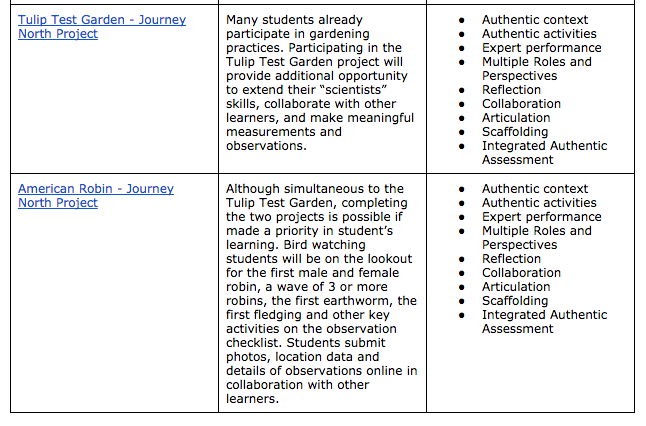
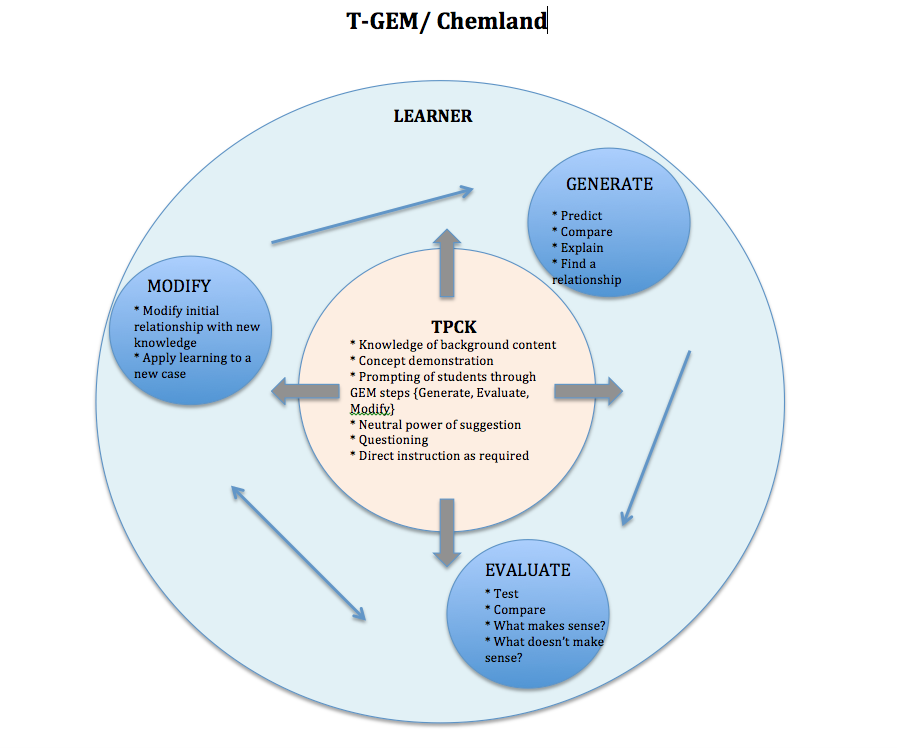
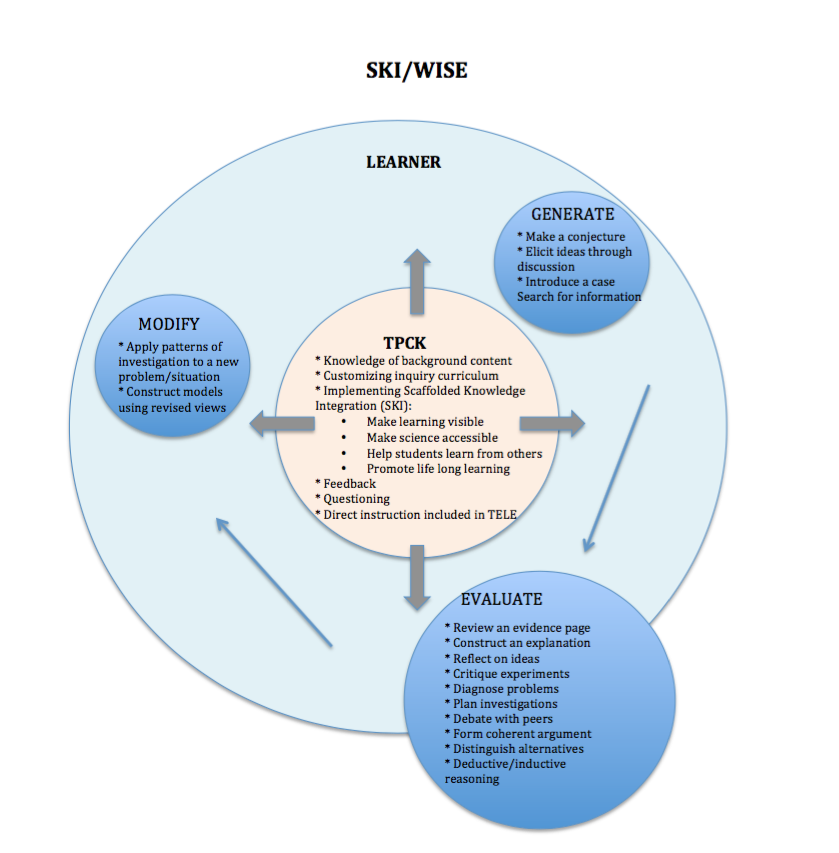
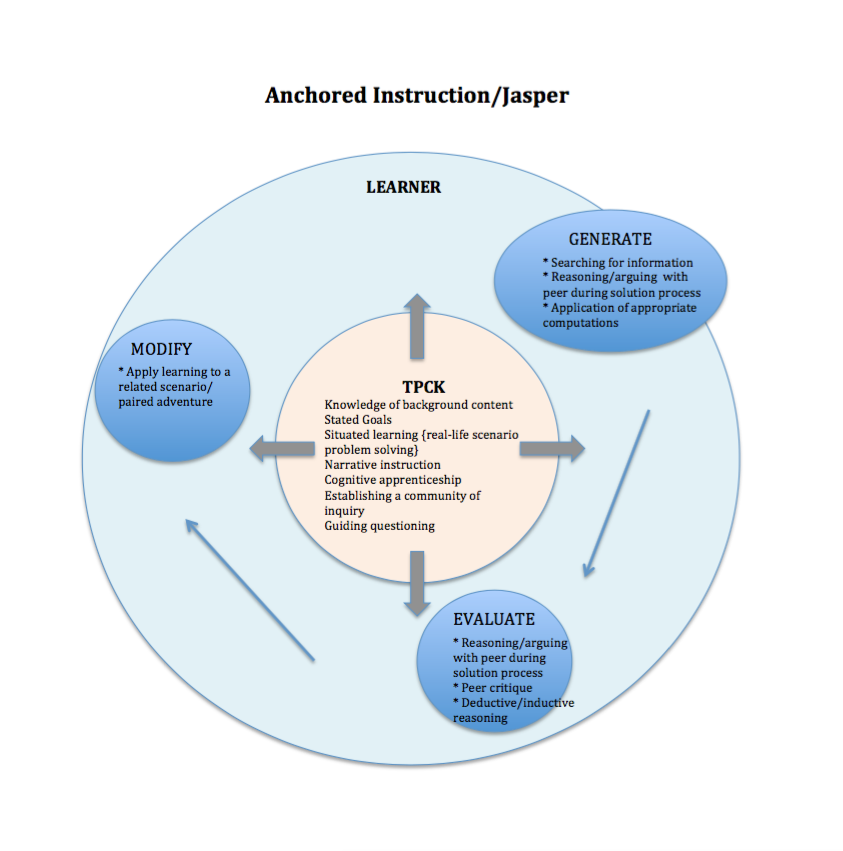
I have been the facilitator of gathering students together to represent the unseen phenomena of molecular movement in states of matter. Students who are “solid” stand very close together and jiggle on the spot, while the “liquid” students stand further apart and move a bit more freely. The students who represent gas find their own space and move around in comparable bliss. I have had students dramatize the story of Archimedes and the king’s golden crown, and have seen a line of students model each part of the ear as sound moves through it. These students are taking on the roles of scientific phenomena, but their role play, as Resnick and Wilensky (1998) would suggest, is merely representing the results rather than “the processes and interactions that give rise to the results” (p.168).
Traditionally role play has found itself in the arts and humanities, helping students view themselves and society through varied lenses, making connections and altering perspectives. Winn (2003) quotes Reyes and Zarama suggesting that in the sciences, too, perspectives of self can be changed. The learned distinctions can often “tell us more about ourselves than about the world we are describing” (Winn, 2003, p.19). As well, Resnick and Wilensky (1998) have found that “role-playing activities provide a framework in which learners can start to make … distinctions – learning to project only the specific parts of their own experiences that are useful for understanding other creatures and objects” (pp.168-9). Can role play in the sciences and mathematics classroom aid in growing these distinctions? In subject areas where traditionally there is one correct answer, can seemingly random and indeterminate role play help bring order and understanding to complex ideas?
Resnick and Wilensky (1998) would affirmatively attest that role play is not intended for simply representing a result, but for “developing new relations with the knowledge underlying the phenomena” (p.167). In fact, they assert that for complex and system sciences, role play is ideal for providing “a natural path for helping learners develop an understanding of the causal mechanisms at work in complex systems. By acting out the role of an individual within a system…, participants can gain an appreciation for the perspective of the individual while also gaining insights into how interactions among individuals give rise to larger patterns of behavior” (p.167). Gaining insights into how localized patterns influence larger-scale, or globalized activity, is essential in understanding the intricacies of a complex system.
The enactivism theory of cognition supports Resnick and Wilensky’s affinity for role play within the sciences and mathematics. As described by Proulx (2013): “[e]nactivism is an encompassing term given to a theory of cognition that views human knowledge and meaning-making as processes understood and theorized from a biological and evolutionary standpoint. By adopting a biological point of view on knowing, enactivism considers the organism as interacting with/in an environment” (p.313). As the organism and environment interact, both change and adapt in response to the interaction, making them even more compatible. This evolution of structure is referred to as coupling (Proulx, 2013). Learning through enactivism is neither simple nor linear, but rather complex and undetermined. Using role play to understand mathematics and complex and science systems takes the student through an evolutionary process of change. The student takes on a role, interacting with the problems (environment) presented, and through this interaction poses new problems and pathways of solution. Along the way, the student finds their initial role is changing too, in order to adapt to the changing environment.
Interestingly, the chaos theory of instructional design also recognizes the value of instruction and learning that is evolutionary in nature (You, 1993). Similarly to Resnick and Wilensky, the chaos theory allows for patterns and order to emerge from seemingly randomness and chaos. You (1993) states that central to the chaos theory is “[t]he discovery that hidden within the unpredictability of disorderly phenomena are deep structures of order” (p.18). Quoting from Hayles (1990, 1991), the characteristics of the chaos theory are described with such phrases as a pattern of order within disorder; chaos is the precursor and partner to order rather than the opposite; and chaos is paradoxically locally random, but stable within a global pattern (You, 1993).
To bring this back to role play in mathematics and sciences, there is a need to recognize that complex ideas can be defined and understood through role play scenarios and interactions whether technology-based or non-technology-based. Through role play, localized complexities can be more clearly defined through continual problem solving and problem posing that allow the learner to begin to see and interpret patterns that emerge. As Proulx (2013) states, “The problems that we encounter and the questions that we undertake are thus as much a part of us as they are part of the environment; they emerge from our interaction with it” (p.315). Perhaps by opening the world of role play to mathematics and science students, we will see more students acting like Barbara McClintock, a Nobel-winning biologist who attributes “her greatest discoveries to the fact that she had a “feeling for the organism” and was able to imagine herself as one of the genes within the corn (Keller, 1983)” (Resnick & Wilensky, 1998, p.168). Perhaps McClintock’s experience is a call for educators to consider further the possibilities for when students are handed permission to relate and interact through imagination, and hence are given opportunity to experience phenomena.
The possible’s slow fuse is lit by the imagination. ~ Emily Dickinson
Resnick, M. & Wilensky, U. (1998) Diving into complexity: Developing probabilistic decentralized thinking through role-playing activities, Journal of the Learning Sciences, 7(2), 153-172. DOI: 10.1207/s15327809jls0702_1
Proulx, J. (2013). Mental mathematics, emergence of strategies, and the enactivist theory of cognition. Educational Studies in Mathematics, 84, 309-328.
Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114.
You, Y. (1993). What can we learn from the chaos theory: An alternative approach to instructional system design. Educational Technology Research and Development 41(3), 17-32. Retrieved from http://www.jstor.org/stable/30218385