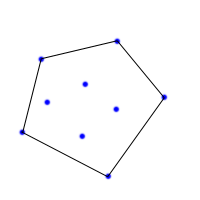
A convex polygon is one where no interior angle is greater than 180°
A convex hull of a set of points is the smallest convex polygon* that contains every one of the points. It is defined by a subset of all the points in the original set. One way to think about a convex hull is to imagine that each of the points is a peg sticking up out of a board. Take a rubber band and stretch it around all of the points. The polygon formed by the rubber band is a convex hull. When interpolating data one should avoid interpolating beyond the convex hull (i.e., extrapolation increases the uncertainty associated with any interpolation).

