Problems for tutorial #1
- Consider the Coop Student/Company Matching Problem: n students apply for jobs at m companies, where company i is looking for ni COOP students. There are at least enough students to fill all of the positions (and there may be too many). Every student has a ranking of companies in order of preference, and each company has a ranking of students in order of preference. An assignment of students to companies is stable if neither of the following situations arises:
- There are two students s and s' and a company c such that s is assigned to c, s' is unemployed, and c prefers s' to s.
- There are two students s and s', and companies c and c', such that s is assigned to c, s' is assigned to c', s prefers c' to c, and c'prefers s to s' (the usual type of instability).
Describe an efficient algorithm that will produce a stable assignment of students to companies, first using a reduction and the Gale-Shapley Algorithm, and then by modifying the G-S Algorithm so that it works directly on this problem.
- Prove or disprove each of the following two statements. That is, either prove that the statement is true, or give an example to show that it is false. Hint: exactly one of the statements is true.
- In every instance of the Stable Matching Problem, there is a stable matching containing a pair (w, m) such that w is ranked first on the preference list of m and m is ranked first on the preference list of w.
- Consider an instance of the Stable Matching Problem in which there exists a man m and a woman w such that m is ranked first on the preference list of w and w is ranked first on the preference list of m. Then in every stable matching S for this instance, the pair (w, m) belongs to S.
- (Induction review) Suppose you begin with a pile of n stones, and split this pile into n piles of one stone each by successively splitting a pile of stones into two smaller piles. Each time you split a pile you multiply the number of stones in each of the two smaller piles you form, so that if these piles have r and s stones in them, respectively, you compute rs. Show that no matter how you split the pile, the sum of the products computed at each step equals n(n-1)/2. Here is an example that shows how the computation proceeds:
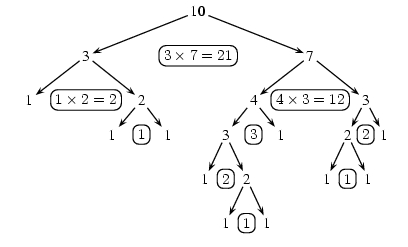
The sum is 21+2+12+1+3+2+2+1+1 = 45, which is indeed 10 * 9 / 2.