- Prove upper and lower bounds on the function T(n) defined by T(n) = 6T(⌊n/2⌋) + 16T(⌊n/4⌋) + 2n3 when n ≥ 4, with T(1) = T(2) = T(3) = 1.
- Consider the problem of taking a sorted array A containing distinct (and not necessarily positive) integers, and determining whether or not there is a position i such that A[i] = i.
- Describe a divide-and-conquer algorithm to solve this problem. Your algorithm should return such a position if it exists, or false otherwise. If A[i] = i for several different integers i, then you may return any one of them.
- Analyze the running time of your algorithm as a function of the number of elements of A.
- King Yéméchan has given his royal mathematician Yséconthé a list of treasures that belong to neighbouring countries. For each treasure, the list specifies
- How much the treasure is worth.
- How easy it would be for Yprantou (the royal thief) to acquire this treasure.
Each treasure can thus be represented by a point in the plane: the x coordinate represents how much the treasure is worth, and the ycoordinate is the difficulty of stealing that treasure (where a higher y coordinate corresponds to a treasure that is easier to steal). Given two such points, we will say that a point q = (q.x, q.y) dominates the point p = (p.x, p.y) if q.x ≥ p.x and q.y ≥ p.y. That is, q lies to the right of and above p, as illustrated in picture on the left.Clearly, a point p that is dominated by a point q is of no interest, since q is both worth more and easier to steal than p. Hence, to help you reach a decision, you only need to worry about locations that correspond to maximal points: those that no other point dominates. For instance, in the picture on the right, the points p3, p4 are p6 are maximal, as you can see from the fact that their upper-right quadrants are empty.

- Describe an algorithm that takes as input a set P of points, and a point q, and returns all points of P that q does not dominate.
- Describe an efficient divide-and-conquer algorithm that takes as input a set P of points, and returns the list of treasures that Yprantou might be asked to steal first (that is, all maximal points of P). Hints:
- Try to divide the problem into two subproblems so that points that are maximal in one of the subproblems are guaranteed to be maximal in P.
- When you are combining the solutions to your subproblems, you should choose a point carefully in one subproblem, and then call your algorithm from part (a) exactly once to eliminate maximal points from the other subproblem that are not maximal in P.
- Analyze the worst-case running time of your algorithm from (b).
Monthly Archives: February 2015
Protected: Tutorial #5 Sample Solutions
Read Before 2015/03/04 Class
- Section 6.2
Read Before 2015/03/02 Class
- Section 6.1 (and the introduction to Chapter 6)
Note that this starts as a divide-and-conquer problem and solution. So, it’s great to read right away (up to page 256’s “memoizing” section).
Assignment #5
PDF document: Assignment #5
Due Monday 2015/03/02 at 5PM in our submission box (#32).
- Use the assignment cover page.
- Read the academic conduct guidelines or expect horrendous consequences for you.
- Please work with a partner; you’ll learn more, and we’ll spend less time on marking and more on making the course awesome.
Protected: Assignment #4 Sample Solution
Slides #11: Deterministic Select
Here’s the PDF of the 2015/02/23 notes.
Tutorial #5 Problems
- Give a recurrence relation for the running time of the following algorithm as a function of n = last – first + 1. To simplify your answer, do not specify the floors and ceilings in your recurrence.
Algorithm TurtleSort(A, first, last) if (last - first ≤ 2) then if (last - first ≤ 1) then if (A[first] > A[first+1]) then swap (A[first], A[first+1]) endif if (last - first = 2) then if (A[last-1] > A[last]) then swap (A[last-1], A[last]) endif if (A[first] > A[first+1]) then swap (A[first], A[first+1]) endif endif endif return endif q1 ← floor of (3*first + last)/4 q2 ← floor of ( first + last)/2 q3 ← floor of ( first + 3*last)/4 turtleSort(A, first, q2) turtleSort(A, q1, q3) turtleSort(A, q2, last) turtleSort(A, q1, q3) turtleSort(A, first, q2) turtleSort(A, q1, q3) - Give a recurrence relation for the running time of the following algorithm as a function of n = last – first + 1. Note that your recurrence relation may have a summation in it.
Algorithm MCM(A, first, last) // // A is an array of objects, rows[X] and columns[X] are // properties of object X whose value is an integer. // if (first = last) then return 0 endif min := +∞ for i := first to last - 1 prod := rows[A[first]] * columns[A[i]] * columns[A[last]]; x := MCM(A, first, i) + MCM(A, i+1, last) + prod; if (x < min ) then min = x endif return min - Using the guess-and-test method, prove that the function T(n) defined by the recurrence relation
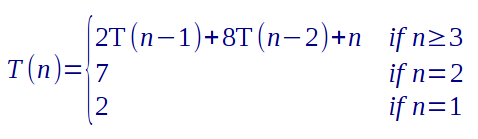
is in O(4n). (Hint: start by proving this bound for the same recurrence without the “+n” part. Then, modify your proof to handle that part.)
Protected: Tutorial #4 Sample Solutions
Read Before 2015/02/23 Class
During Reading Break, I thought we should have some reading 🙂
Please read:
- Section 5.3
- Section 5.4
We’ll likely finish Chapter 5 at that point.
Next, we’ll either continue discussing Divide and Conquer for a while with limited new readings (perhaps one or both of the remaining sections) or we’ll move on to Chapter 6.
Since we’re definitely moving on to Chapter 6 eventually, if you want to read ahead, I recommend starting with 6.1 to 6.4 on the completely awesome topic of Memoization and Dynamic Programming.