This problem is based on 8.4 from the Kleinberg and Tardos textbook.

Suppose you’re consulting for a group that manages a high-performance real-time system in which asynchronous processes make use of shared resources. Thus, the system has a set of n processes and a set of m resources. Each process specifies a set of resources that it requests to use. Each resource might be requested by many processes at once, but it can only be used by a single process at a time.

Your job is to allocate resources to processes that request them. If a process is allocated all the resources it requests, then it is active; otherwise, it is blocked. You want to perform the allocation so that as many processes as possible are active.

Thus, we phrase the Resource Reservation Problem (RR) as follows: Given a set of processes and resources, the set of requested resources for each process, and a number k, is it possible to allocate resources to processes so that at least k processes will be active?

1. For this part and the next part only, assume you do have a polynomial-time algorithm for RR. Give a polynomial-time algorithm to determine the largest k for which you can allocate resources to processes so that at least k processes will be active.
2. Still assuming you have a polynomial-time algorithm for RR, give a polynomial-time algorithm to determine a maximum-size set of processes that can be simultaneously active. (The specific processes, not just how many there are.)
3. Now stop assuming you have a polynomial-time algorithm for RR, and consider the following list of problems. For each problem either give a polynomial-time algorithm or prove that the problem is NP-complete. (In the former case, your “algorithm” may be a reduction to another problem that you know can be solved in polynomial time. Hint: One of these can be solved in polynomial time by reduction to the “maximum matching problem”, which can be solved in polynomial time.)
   1. The general Resource Reservation Problem defined above.
   2. The special case of the problem when k = 2.
   3. The special case of the problem when k = 10.
   4. The special case of the problem when there are two types of resources—say, robotic dogs and robotic cats—and each process requires exactly one resource of each type. (In other words, each process requires one specific robotic dog and one specific robotic cat.)
   5. The special case of the problem when each resource is requested by at most two processes.

Provide a recurrence relation for the quantity described in each of the following problems. For each one, also indicate either a memoized or dynamic programming approach to solving the recurrence and analyse its efficiency. (Do DP at least once. Remember that it’s the harder one because you must order the subproblems “manually” and so worth a bit of extra practice.)

1. Let G = (V, E) be an undirected graph with n nodes. A subset of the nodes is called an independent set if no two of them are joined by an edge. Finding large independent sets is difficult in general, but it can be done efficiently if the graph is simple enough.

   Let us call the graph G a path if its nodes can be written as v₀, v₁, …, v_n-1 with an edge between v_i and v_j if and only if the numbers i and j are consecutive. With each node v_i we associate a positive integer weight w_i. For example, in the following path, the weights are the numbers drawn inside the nodes.

   

   Define recurrence relations for

   • With[i]: the maximum sum we can obtain using non-consecutive elements from v₀, …, v_i, including the element v_i in the sum.
   • Without[i]: the maximum sum we can obtain using non-consecutive elements from v₀, …, v_i, without including the element v_i in the sum.
2. There are many sunny Spring days in Vancouver. Unfortunately, this year, it is raining on the day of the CSSS (CS student society) boat cruise and dinner. The CSSS president decides to rebook the cruise for another day, and needs to contact everybody who has made reservations. Luckily, every student made his/her reservation by talking to another student who had already made his/hers. That is, the students who have reservations for the cruise form a tree, whose root is the CSSS president!

   To notify everyone of the postponement, the CSSS president first calls each of the students who bought their tickets directly from him/her, one at a time (his/her “children”). As soon as one of these students has been notified, he/she can then notify all of his/her “children”.

   We can picture this process as being divided into rounds. In one round, each person who has already learned of the postponement can call one of his/her children. The number of rounds it takes for everyone to be notified depends on the sequence in which each person makes their phone calls. For instance, in the following figure, it will take only two rounds if A calls B first, but three rounds if A starts by calling D (note that A can not call C directly).

   

   Write a recurrence relation for R(N), the minimum number of rounds needed to inform all descendants of a node N.

3. As some of you know well, and others of you may be interested to learn, a number of languages (including Chinese and Janapese) are written without spaces between the words. Consequently, software that works with text written in these languages must address the word segmentation problem: inferring likely boundaries between consecutive words in the text. If English were written without spaces, the analogous problem would consist of taking a string like “meetaeight” and deciding that the best segmentation is “meet at eight” (and not “me et at eight”, or “meet ate ight”, or any of the huge number of even less plausible alternatives). How could we automate this process?A simple approach that is at least reasonably effective is to find a segmentation that simply maximizes the cumulative “quality” of its individual constituent words. Thus, suppose you are given a black box that for any string of letters x = x₀, x₁, …, x_k will return a number Q(x). This number can be either positive or negative; larger numbers correspond to more plausible English words. So Q(me) would be positive, while Q(ght) would be negative.

   Given a long string of letters y = y₀, y₁, …, y_n-1, a segmentation of y is a partition of its letters into contiguous blocks of letters; each block corresponds to a word in the segmentation. The total quality of a segmentation is determined by adding up the qualities of each of its blocks. So we would get the right answer for the problem above provided that Q(meet) + Q(at) + Q(eight) was greater than the total quality of any other segmentation of the string.

   Give a recurrence relation for TQ(i): the maximum total quality of any segmentation of the letters y₀, y₁, …, y_i. Hint: look for the position of the first letter of the current “word”.

1. Prove upper and lower bounds on the function T(n) defined by T(n) = 6T(⌊n/2⌋) + 16T(⌊n/4⌋) + 2n³ when n ≥ 4, with T(1) = T(2) = T(3) = 1.
2. Consider the problem of taking a sorted array A containing distinct (and not necessarily positive) integers, and determining whether or not there is a position i such that A[i] = i.
   1. Describe a divide-and-conquer algorithm to solve this problem. Your algorithm should return such a position if it exists, or false otherwise. If A[i] = i for several different integers i, then you may return any one of them.
   2. Analyze the running time of your algorithm as a function of the number of elements of A.
3. King Yéméchan has given his royal mathematician Yséconthé a list of treasures that belong to neighbouring countries. For each treasure, the list specifies
   • How much the treasure is worth.
   • How easy it would be for Yprantou (the royal thief) to acquire this treasure.

   Each treasure can thus be represented by a point in the plane: the x coordinate represents how much the treasure is worth, and the ycoordinate is the difficulty of stealing that treasure (where a higher y coordinate corresponds to a treasure that is easier to steal). Given two such points, we will say that a point q = (q.x, q.y) dominates the point p = (p.x, p.y) if q.x ≥ p.x and q.y ≥ p.y. That is, q lies to the right of and above p, as illustrated in picture on the left.Clearly, a point p that is dominated by a point q is of no interest, since q is both worth more and easier to steal than p. Hence, to help you reach a decision, you only need to worry about locations that correspond to maximal points: those that no other point dominates. For instance, in the picture on the right, the points p₃, p₄ are p₆ are maximal, as you can see from the fact that their upper-right quadrants are empty.

   

   1. Describe an algorithm that takes as input a set P of points, and a point q, and returns all points of P that q does not dominate.
   2. Describe an efficient divide-and-conquer algorithm that takes as input a set P of points, and returns the list of treasures that Yprantou might be asked to steal first (that is, all maximal points of P). Hints:
      • Try to divide the problem into two subproblems so that points that are maximal in one of the subproblems are guaranteed to be maximal in P.
      • When you are combining the solutions to your subproblems, you should choose a point carefully in one subproblem, and then call your algorithm from part (a) exactly once to eliminate maximal points from the other subproblem that are not maximal in P.
   3. Analyze the worst-case running time of your algorithm from (b).

1. Give a recurrence relation for the running time of the following algorithm as a function of n = last – first + 1. To simplify your answer, do not specify the floors and ceilings in your recurrence.

   Algorithm TurtleSort(A, first, last)
   
   if (last - first ≤ 2) then
       if (last - first ≤ 1) then
           if (A[first] > A[first+1]) then
               swap (A[first], A[first+1])
           endif
   
           if (last - first = 2) then
               if (A[last-1] > A[last]) then
                   swap (A[last-1], A[last])
               endif
               if (A[first] > A[first+1]) then
                   swap (A[first], A[first+1])
               endif
           endif
       endif
       return
   endif
   
   q1 ← floor of (3*first +   last)/4
   q2 ← floor of (  first +   last)/2
   q3 ← floor of (  first + 3*last)/4
   
   turtleSort(A, first, q2)
   turtleSort(A, q1, q3)
   turtleSort(A, q2, last)
   turtleSort(A, q1, q3)
   turtleSort(A, first, q2)
   turtleSort(A, q1, q3)
   

2. Give a recurrence relation for the running time of the following algorithm as a function of n = last – first + 1. Note that your recurrence relation may have a summation in it.

   Algorithm MCM(A, first, last)
   //
   // A is an array of objects, rows[X] and columns[X] are  
   // properties of object X whose value is an integer.
   //
   if (first = last) then
   	return 0
   endif
   
   min := +∞
   for i := first to last - 1
   	prod := rows[A[first]] * columns[A[i]] * 
                   columns[A[last]];
   	x := MCM(A, first, i) + MCM(A, i+1, last) + prod;
   
   	if (x < min ) then
   	    min = x
   	endif
   return min
   

3. Using the guess-and-test method, prove that the function T(n) defined by the recurrence relation
   
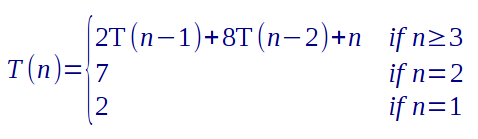
   is in O(4ⁿ). (Hint: start by proving this bound for the same recurrence without the “+n” part. Then, modify your proof to handle that part.)