- Give a recurrence relation for the running time of the following algorithm as a function of n = last – first + 1. To simplify your answer, do not specify the floors and ceilings in your recurrence.
Algorithm TurtleSort(A, first, last) if (last - first ≤ 2) then if (last - first ≤ 1) then if (A[first] > A[first+1]) then swap (A[first], A[first+1]) endif if (last - first = 2) then if (A[last-1] > A[last]) then swap (A[last-1], A[last]) endif if (A[first] > A[first+1]) then swap (A[first], A[first+1]) endif endif endif return endif q1 ← floor of (3*first + last)/4 q2 ← floor of ( first + last)/2 q3 ← floor of ( first + 3*last)/4 turtleSort(A, first, q2) turtleSort(A, q1, q3) turtleSort(A, q2, last) turtleSort(A, q1, q3) turtleSort(A, first, q2) turtleSort(A, q1, q3) - Give a recurrence relation for the running time of the following algorithm as a function of n = last – first + 1. Note that your recurrence relation may have a summation in it.
Algorithm MCM(A, first, last) // // A is an array of objects, rows[X] and columns[X] are // properties of object X whose value is an integer. // if (first = last) then return 0 endif min := +∞ for i := first to last - 1 prod := rows[A[first]] * columns[A[i]] * columns[A[last]]; x := MCM(A, first, i) + MCM(A, i+1, last) + prod; if (x < min ) then min = x endif return min - Using the guess-and-test method, prove that the function T(n) defined by the recurrence relation
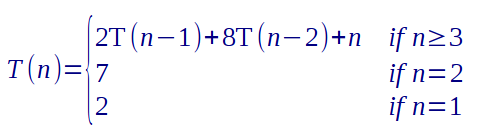
is in O(4n). (Hint: start by proving this bound for the same recurrence without the “+n” part. Then, modify your proof to handle that part.)
Tutorial #5 Problems
Leave a reply