Hello all,
A belated Happy New Year to all (note the logical form: year is NOT plural, except apparently in North America)!
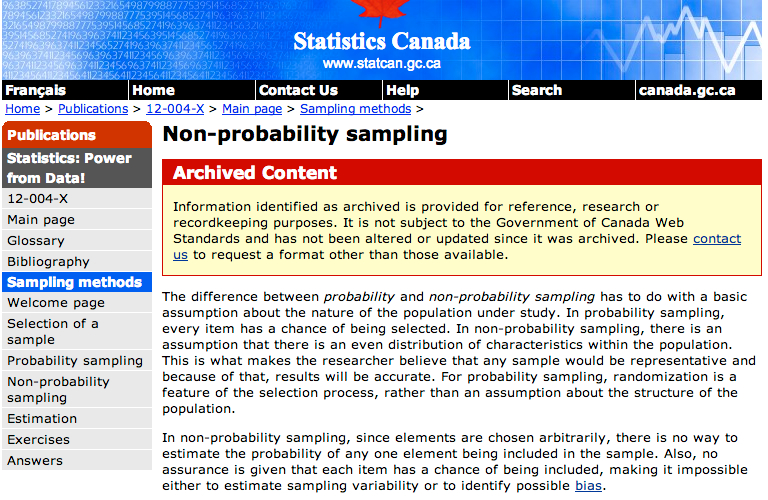
We thought we would kick off the year with a quick discussion on sampling theory as it seems a subject fraught with confusion. To illustrate this point I note a section from the Statistics Canada website which was cited to me last year by a graduate student (postgrad for readers in Blighty). The Stats Canada site notes the following about non-probability sampling:
Now I certainly don’t claim to be a statistical expert as my expertize with inferential statistics is fairly limited. But I have a bit of a logic background from programming, so I do know a little about logical clauses. The problematic part for me is:
“in non-probability sampling, there is an assumption that there is an even distribution of characteristics within the population. This is what makes the researcher believe that any sample would be representative and because of that, results will be accurate.”
Something about that didn’t seem quite right, and it seems inconsistent with the later statement:
“in non-probability sampling, since elements are chosen arbitrarily, there is no way to estimate the probability of any one element being included in the sample.”
Logically, if it is a non-probability sample, then the sample will not be representative of the probability of a phenomenon being present in a population. If a phenomenon is equally evident in all members of the population then it is a probability sample as the sample is subject to probabilistic inference. In the case of everyone demonstrating the phenomenon the probability of finding it in your sample would be 100%. In effect, if the first statement is true, then the second cannot be as they are mutually exclusive. I believe what they are trying to suggest, is that a non-probability sample is a targeted sample, selected to include from a frame (the set of people from whom the sample are drawn) who all exhibit the same characteristic, or have experiences the same phenomenon. Technically, this is not the same as an “even-distribution” though.
The way I was taught, and understand the difference between probability, and non-probability samples is as follows (and is also consistent with the second clause).
Non-Probability Sampling
Non-probability sampling does not depend upon the rationale of probability theory, and with it there is no way to estimate the likelihood for any particular element being included within a sample. Researchers may use this approach when a representative sample is unnecessary (such as to explore the existence of a phenomena or determine personal experience), or when a probability sample is unavailable. Even with samples that are not representative of a population we can still explore the elements to describe phenomena or identify if a particular phenomenon exits.
Non-probability sampling may be useful in qualitative work, or for practicality such as in focus group selection. Non-probability sampling is also useful if there is a limited population size, as with very small frames the key statistical properties required to support a probability sample do not exist. E.g., surveying 20 users of a new tool in a specialty clinic. It may also be a useful technique where the frame parameters are uncertain. E.g., sampling street drug users. Techniques for non-probability sampling are summarized as follows:
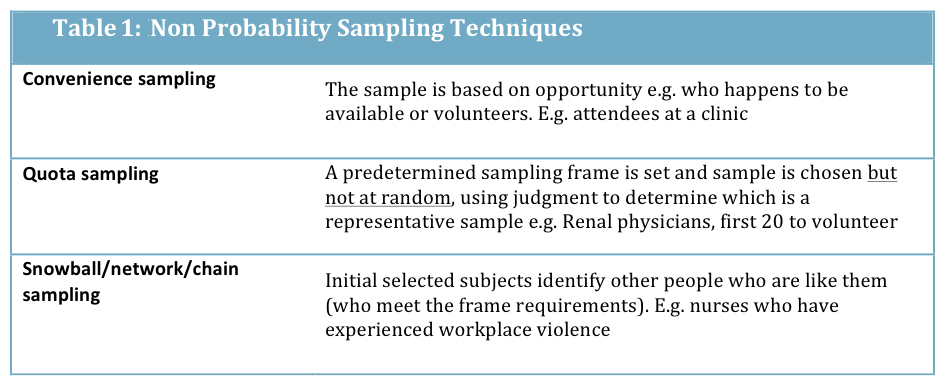
Probability Sampling
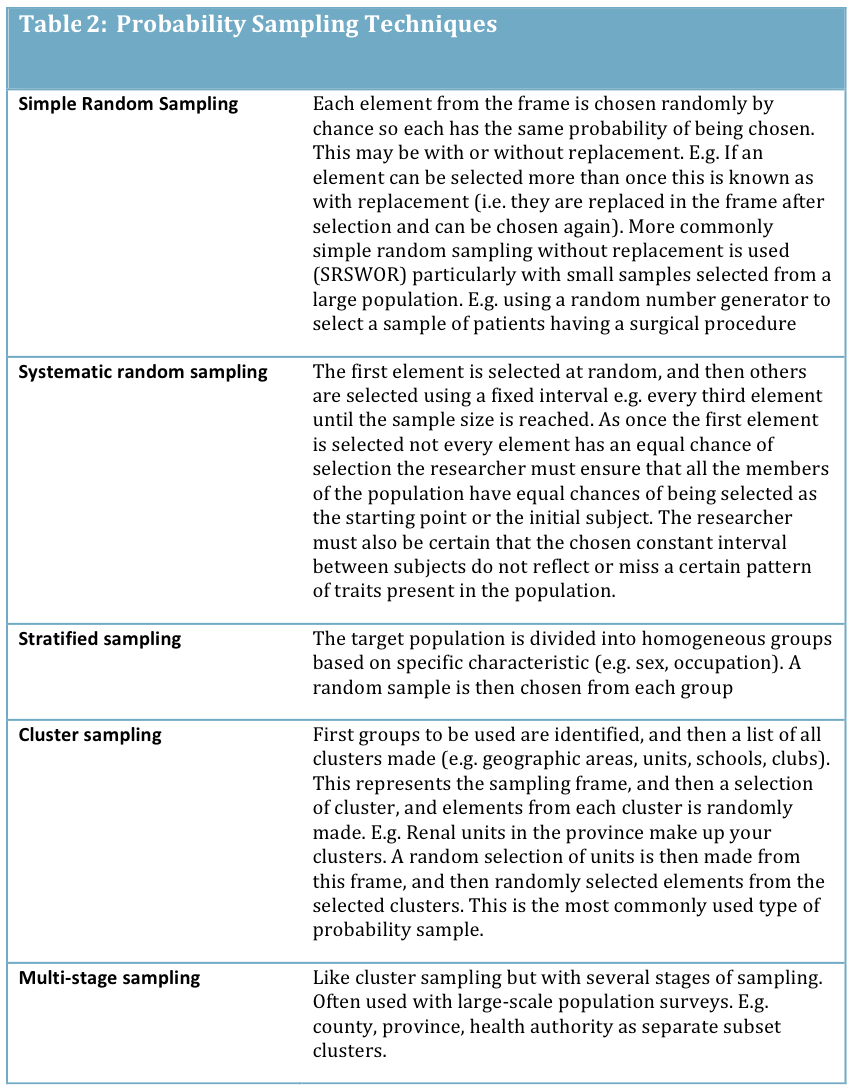
Probability sampling is more commonly used in quantitative research and aims to use representative samples of a whole. It is based on probability theory and accepted statistical principles to allow the prediction that findings observed in the sample will occur in the whole population. It requires that every element has the chance of being selected, ideally (but not necessarily) an equal chance. In this type of sampling the probability of selection of an element can be calculated, so a sample element can be weighted as necessary to give it unbiased representation. It also requires that random chance determine selection. In the case of random samples, mathematical theory is available to assess the sampling error. Thus, estimates obtained from random samples can be accompanied by measures of the uncertainty associated with the estimate e.g., standard error or confidence intervals. Examples of probability sampling techniques are summarized as follows:
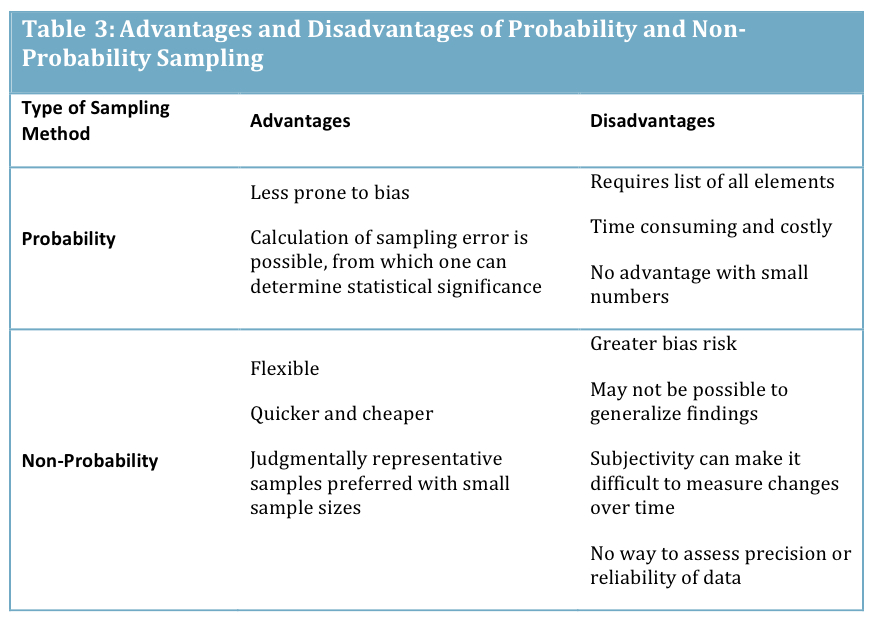
This seems consistent with the literature I have looked at on the subject over the years (such as Lenth, 2001; Campbell, Machin & Walters, 2007; Polit & Beck, 2014). The advantages and disadvantages of both approaches can be summarized as:
I did write to Stats Canada, asking for an clarification, and even politely suggested a possible correction that would make their description consistent. However, I never heard back, so I guess they don’t have time to answer the blathering of an inquisitive nursing professor.
I then asked a couple of stats savvy colleagues if they could explain the apparent inconsistency. One said, “Err, that doesn’t seem right to me” and another “Well, if Stats Canada say so it must be right!” Therefore I am am none the wiser to their rationale. All I can say is from the good science perspective: never take for granted anything you read (from whatever source, and well, especially on the web)!
If any stats wizards ever read this blog please do pitch in and give us your thoughts.
Onwards and Upwards
Bernie
References
Campbell M.J., Machin D. & Walters S., (2013) Medical Statistics: A Textbook for the Health Sciences. Chichester, John Wiley.
Lenth, R.V. (2001). Some practical guidelines for effective sample size determination. The American Statistician, 55, 187-193.
Polit B.F. & Beck C.T. (2014) Essentials of Nursing Research: Appraising Evidence for Nursing Practice. New York. Wolters Kluwer

 Follow
Follow