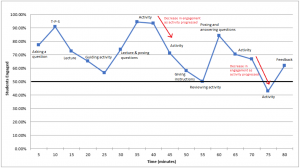
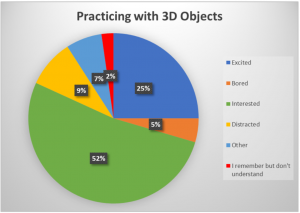
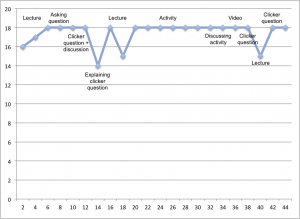
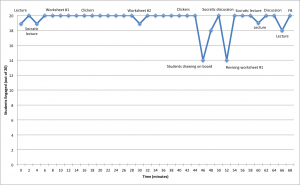
My final observation for CATL was completed in a course that I’m very familiar with: ISCI 330A – Symmetry. The instructor for this course is not one of my mentors for CATL, but I’ve been his TA for this course four times, and was a co-instructor with him twice for the version of the course that was run through the Vancouver Summer Program. I also completed one of my practicum lessons for this term in his class. The Symmetry class has about 40 students that are mostly in third year. It is not a required course for Integrated Sciences students, but it can be used as one of a certain number of Integrated Sciences courses that they are required to take for their degree. Because of this, I would think that many of the students are in the course because they want to be, and not because it’s required. This could increase their motivation to do well in the course and participate in the lessons. Also, teaching symmetry naturally involves incorporating active learning into the lesson, so the lesson involved lots of hands-on work identifying symmetry operations in various 3-dimensional shapes.
The lesson that I observed was on 3-dimensional point groups and built on the material that I had covered in the previous lesson for my practicum. I’ve also taught this specific lesson in the past, so I was aware of the challenges associated with the content. This class covers something called “roto-inversions”, which is a symmetry operation that involves both rotation and an inversion through the centre of the object. Roto-inversions are not only difficult to comprehend in theory for many students, but they are often difficult to identify in the 3-dimensional objects that students are working with, even after lots of practice. To help students visualize roto-inversions, the instructor showed the students some tricks to identify each type of roto-inversion, instead of just telling students what the different roto-inversions look like. He created representations of the objects on his PowerPoint slides and stepped through the motions sequentially to demonstrate which part of the object had a distinct feature. Then, he showed them real examples of objects that contained each of the roto-inversions they were learning, and reiterated the tricks to identify them. He even built a giant version of a 3-dimensional object containing a 4-fold roto-inversion to make the symmetry operation easier to see. I think showing the objects to the students did help them see the roto-inversions, but students sitting at the back of the classroom may not have gotten a good enough view of the objects to see what was going on. This could be solved by moving around the room with the objects to ensure that all students got a chance to see it up close.
I was happy to see that the instructor has continued to ask ABCD card questions during his lessons. I had first started using ABCD cards in Symmetry last year after one of my mentors suggested I try them out since we didn’t have an iclicker base in the classroom. I then showed them to the instructor and provided him with the file to print out his own cards. He seems interested in continuing to use ABCD cards and has also expressed interest in incorporating iclickers into his lessons in place of the ABCD cards. I’m going to try and get an iclicker base for this classroom so that he can start to use clickers in this course and also in the other course that he teaches in the January semester. Personally, I find iclickers easier to use than ABCD cards, particularly because there are less issues with anonymity. This instructor has never used iclickers before, but he seems eager to try them out and learn the proper techniques to meaningfully incorporate them into a lesson.
In the future, I’d like to keep attending this instructor’s Symmetry classes to see any changes he makes to his lessons. He seems to be starting to incorporate more active learning into his lessons, and I’d like to see how that develops. I’d also like to continue to engage in conversations with him about teaching techniques that he could consider implementing in his courses.