Introduction to Limits
Limits are a core feature of calculus, and they help us determine the nearest points closest to a specific point on a graph. Limits give us the possibility to find the closest point possible to an exact value, without ever reaching that value. As well, limits will help us build the definitinon of the derivative which will help us differentiate eqations and find the slopes of graphs. This is what a typical limit notation looks like:
Examples of Limits
Below is an image of the graph f(x). If we look for the limit at x=1 of this graph, it is 6 l i m x → 1 f ( x ) = 6 {\displaystyle \displaystyle lim_{x\to 1}f(x)=6} . Also, since the graph is continous at this point, the value of x=1 is also 6.
Now looking at the same graph, the limit at x=2 is 4 l i m x → 2 f ( x ) = 4 {\displaystyle \displaystyle lim_{x\to 2}f(x)=4} , while the value at x=2 is not existent.
Positive and Negative Sides of Limits
Limits can exist as both the positive side (towards positive infinity), or as the negative side (towards negative infinity). In the graph below, the negative limit at x=1 is 2 l i m x → 1 − f ( x ) = 2 {\displaystyle \displaystyle lim_{x\to 1-}f(x)=2} , while the positive limit of x=1 is 4 l i m x → 1 + f ( x ) = 4 {\displaystyle \displaystyle lim_{x\to 1+}f(x)=4} . The value of x=1 is 2.
Worked Out Simple Limit Problems
- Substitution
lim x → 2 2 x + 1 = ( 2 ) ( 2 ) + 1 = 5 {\displaystyle \lim _{x\to 2}2x+1=(2)(2)+1=5}
- Factoring
lim x → 3 x 2 − 9 x − 3 = lim x → 3 ( x + 3 ) ( x − 3 ) ( x − 3 ) = lim x → 3 ( x + 3 ) = 6 {\displaystyle \lim _{x\to 3}{\frac {x^{2}-9}{x-3}}=\lim _{x\to 3}{\frac {(x+3)(x-3)}{(x-3)}}=\lim _{x\to 3}(x+3)=6}
- Common Denominator
lim x → 0 1 x + 3 − 1 3 x = lim x → 0 3 − ( x + 3 ) 3 ( x + 3 ) x = lim x → 0 − x 3 ( x + 3 ) 1 x = lim x → 0 − 1 3 ( x + 3 ) = − 1 3 ( 0 + 3 ) = − 1 9 {\displaystyle \lim _{x\to 0}{\frac {{\frac {1}{x+3}}-{\frac {1}{3}}}{x}}=\lim _{x\to 0}{\frac {\frac {3-(x+3)}{3(x+3)}}{x}}=\lim _{x\to 0}{\frac {-x}{3(x+3)}}{\frac {1}{x}}=\lim _{x\to 0}{\frac {-1}{3(x+3)}}={\frac {-1}{3(0+3)}}={\frac {-1}{9}}}
- Radicals
lim
x
→
0
x
+
1
−
1
x
{\displaystyle \lim _{x\to 0}{\frac {{\sqrt {x+1}}-1}{x}}}
lim x → 0 x + 1 − 1 x x + 1 + 1 x + 1 + 1 = lim x → 0 x + 1 − 1 x ( x + 1 + 1 = lim x → 0 x x ( x + 1 + 1 ) = lim x → 0 1 x + 1 + 1 = 1 0 + 1 + 1 = 1 2 {\displaystyle \lim _{x\to 0}{\frac {{\sqrt {x+1}}-1}{x}}{\frac {{\sqrt {x+1}}+1}{{\sqrt {x+1}}+1}}=\lim _{x\to 0}{\frac {x+1-1}{x({\sqrt {x+1}}+1}}=\lim _{x\to 0}{\frac {x}{x({\sqrt {x+1}}+1)}}=\lim _{x\to 0}{\frac {1}{{\sqrt {x+1}}+1}}={\frac {1}{{\sqrt {0+1}}+1}}={\frac {1}{2}}}
Additional practice: http://lee-apcalculus.weebly.com/uploads/1/3/0/4/13041727/limits_algebraically.pdf
Limit Rules
Below is a screenshot of all the possible limit rules.
Limit Definition of Derivative
The definition of the derivative, using limits, allows us to find the derivative of a graph without needing to use differentiation methods. By understanding the definition of the derivative, you will be able to differentiate any equation.
There exist two different definitions of the derivative. While both are very useful, the second method below, will allow you to complete differentiations with the minimum amount of information.
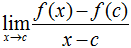
Note: the c variable in this exation may be replaced with the variable a
Worked Out Problems Using Both Definitions
When asked to find the derivative of an equation, use
When asked to find the derivative @ x=c where c is a number, use
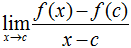
- Find the derivative of the function
x
x
+
5
{\displaystyle {\frac {x}{x+5}}}
using the definition of a derivative.
lim
x
→
0
x
+
h
x
+
h
+
5
−
x
x
+
5
h
=
lim
x
→
0
(
x
+
h
)
(
x
+
5
)
−
(
x
)
(
x
+
h
+
5
)
(
x
+
h
+
5
)
(
x
+
5
)
1
h
{\displaystyle \lim _{x\to 0}{\frac {{\frac {x+h}{x+h+5}}-{\frac {x}{x+5}}}{h}}=\lim _{x\to 0}{\frac {(x+h)(x+5)-(x)(x+h+5)}{(x+h+5)(x+5)}}{\frac {1}{h}}}
=
lim
x
→
0
x
2
+
5
x
+
x
h
+
5
h
−
x
2
−
x
h
−
5
x
(
x
+
h
+
5
)
(
x
+
5
)
1
h
{\displaystyle =\lim _{x\to 0}{\frac {x^{2}+5x+xh+5h-x^{2}-xh-5x}{(x+h+5)(x+5)}}{\frac {1}{h}}}
=
lim
x
→
0
5
h
(
x
+
h
+
5
)
(
x
+
5
)
{\displaystyle =\lim _{x\to 0}{\frac {5h}{(x+h+5)(x+5)}}}
sub in h=0 we get
5
(
x
+
5
)
2
{\displaystyle {\frac {5}{(x+5)^{2}}}}
- Find the derivative of f(x) at x=1 where
f
(
x
)
=
4
x
+
12
{\displaystyle f(x)={\sqrt {4x+12}}}
lim
x
→
1
f
(
x
)
−
f
(
1
)
x
−
a
=
lim
x
→
1
4
x
+
12
−
4
x
−
1
{\displaystyle \lim _{x\to 1}{\frac {f(x)-f(1)}{x-a}}=\lim _{x\to 1}{\frac {{\sqrt {4x+12}}-4}{x-1}}}
=
lim
x
→
1
4
x
+
12
−
4
x
−
1
4
x
+
12
+
4
4
x
+
12
+
4
{\displaystyle =\lim _{x\to 1}{\frac {{\sqrt {4x+12}}-4}{x-1}}{\frac {{\sqrt {4x+12}}+4}{{\sqrt {4x+12}}+4}}}
=
lim
x
→
1
4
x
+
12
−
16
(
x
−
1
)
(
4
x
+
12
+
4
)
{\displaystyle =\lim _{x\to 1}{\frac {4x+12-16}{(x-1)({\sqrt {4x+12}}+4)}}}
=
lim
x
→
1
4
x
+
4
(
x
−
1
)
(
4
x
+
12
+
4
{\displaystyle =\lim _{x\to 1}{\frac {4x+4}{(x-1)({\sqrt {4x+12}}+4}}}
=
lim
x
→
1
(
4
)
(
x
−
1
)
(
x
−
1
)
(
4
x
+
12
+
4
)
=
1
2
{\displaystyle =\lim _{x\to 1}{\frac {(4)(x-1)}{(x-1)({\sqrt {4x+12}}+4)}}={\frac {1}{2}}}
Additional practice:
https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/limcondirectory/LimitConstant.html
https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/liminfdirectory/LimitInfinity.html
The Three Requirements of Continuity
1. All points on the given interval must be continuous
2. For a point to be continuous, the limit of each point must equal the value at the designated point
3. For Requirement 2 to exist, a limit must exist, therefore the left hand side limit and the right hand side limit must be equal.
Below is a picture which shows three different points on a graph. We will go through each point.
To begin we will look at the x-coordinate of (-2). At this point the graph is discontinuous because Requirement 3 is not met. The left hand limit does not equal the right hand limit, and such the limit cannot exist.
Next, at x-coordinate (0), the graph is continuous. This is true because both the left hand side and right hand side limits exist, and the value of the limit of the function equals the value of the designated point.
Finally, let's look at at x-coordinate (3). At this point the graph is discontinuous because Requirement 2 is not met. Although both left hand side and right hand side limits are equal, the value of the limit does not equal the value of the function at that point.
Examples of Singularities
In the function above, the value of f(1) does not exist and as well the limits do not exists. Due to the nature of the graph, it is seen as a singularity at this point.
In the function above, the value of f(0) does not and the limits also do not exist. This case is again called a singularity due to the nature of the function.