Introduction to Taylor Polynomials
Taylor Polynomials will help us approximate values of a specific function without using a calculator to do so. To begin, we will look at Linear Approximation and then follow with Taylor Polynomials.
Linear Approximation
Linear Approximation requires us to know a certain point on a function, and using this point and a tangent line of the particular function tangent to this point, we will be able to approximate values on the function in a very close proximity to the centre of the tangent line. One problem with the linear approximation is that as we move father from the initial centre of the tangent line, the approximation can create high error margins.
Steps for Linear Approximation
1. Determine the derivative of the function of which you wish to approximate. This
2. Plug in the value you wish to approximate into the linear tangent function.
!Note!: Linear approximation is just a stepping stone to Taylor polynomials. It is used to show how Taylor Polynomials will operate and function.
Video on Linear Approximation
Taylor Polynomials
Taylor Polynomials function around the premise of this equation.
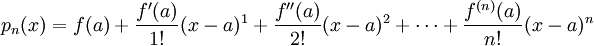
Where:
a = the centre value (usually given, or easy attainable)
x = the value at which you wish to approximate the function
In order to approximate using a Taylor series, follow the formula. Usually in MATH 104 and 184 held at UBC you will not need to approximate past the 3rd degree, which means the first 3 terms in the formula. After solving for the general equation (x and a still as variables) plug in the centre point of the Taylor series (usually the one given in the question) and the point at which you wish to approximate.
Attention. Make sure you know how the factorial system works (example 4!= 4*3*2*1)
Khan Academy Video Explaining the Taylor Polynomials
Approximation Error
Some questions may ask you if the approximate is greater or less than the actual value. This question will only be asked if you are asked to find the 2nd degree Taylor Polynomial, or the straight line tangent. Here are the steps
1. Use the equation of the function given and perform the second derivative test.
2. Compare with the 2nd degree Taylor Polynomial.
2a. If the second derivative test yields a negative, that means that the graph will slope down thus ensuring that the 2nd degree Taylor estimate is greater
2b. If the second derivative test yields a positive, that means that the graph will slope up thus ensuring that the 2nd degree Taylor estimate is smaller
Equation for Error
Here is a video explaining and showing the equation for calculating the error of a Taylor Polynomial estimate.
This is the formula:
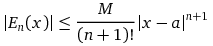
Video
