Technical Definitions: Bandstructure

Introduction

The purpose of this assignment is to not only appreciate the need for technical definitions, but to understand the necessity of considering a non-technical audience when defining complex terms. The assignment itself will have 3 parts:

1. to choose a complex technical term relating to my professional field
2. to create a hypothetical situation and an audience of non-technical readers for which we will write to explaining our technical term
3. create a definition for our technical term using three different defining techniques:
   1. via a parenthetical definition
   2. via a sentence definition
   3. via an expanded definition

The expanded definition should contain 4 different expansion strategies as listed in Technical Communication: 14th Edition, as well as at least one visual, and no fewer than three outside references (cited in MLA or APA style). The expansion strategies that I used are: operating principle, analysis of parts, comparison and contrast, examples, and visuals.

Technical Terms and Definitions

Technical Term: Bandstructure

Situation: Dr. Alana Ginsley works as a physics professor for a first year course. While most of her students are familiar with the concept of conductors, insulators and semiconductors, she wants them to understand exactly how it is that materials can behave in different way. She is putting together an article that will define the concept of “bandstructure”, using simple language that requires no knowledge of quantum mechanics or solid state physics.

Audience: The intended audience, who have a high school level knowledge of physics and chemistry, are familiar with the concept of conductors and insulators, but may not know why exactly the materials behave differently. Many of these students do not intend to pursue solid state physics, so while it is important to educate the audience about bandstructure, it does not have to be so descriptive as to make the audience confused.

 

Band Structure

Bandstructure (the allowed energies that electrons are allowed to occupy in a material) describes how electrons can move within a certain medium. It is a property of materials that describes how electrons are bound to atoms and explains whether the material can conduct electricity. To fully understand how bandstructure works we first have to realize how different elements are formed, and then how the electrons of these elements behave when materials are formed.

You may remember from prior courses that atoms are made up of protons, neutrons, and electrons. Elements are defined by the number of protons in their nucleus, but most stable elements will have the same number of electrons as protons.  When talking about bandstructure, we will talk mostly of electrons. According to quantum mechanics, electrons are only allowed to exist in discrete energy states, surrounding the nucleus, and only a certain amount of electrons can exist in each state. These states correspond to a different energy, and the lowest energy states fill up with electrons first. Now, say we take many many atoms of different elements and make a solid material out of it.

The electrons in this material will organize themselves so they can only exist in different bands of energy.  Whether this material can conduct or not has to do with the band structure of the material, and like before, the electrons fill up the lowest energy bands first. The most notable aspects of a material’s band structure is the conducting band, and the valence band (see fig. 1), which is the two highest bands of energy before all the electrons have been  “placed” in the different energy potentials. Strictly speaking, all bands with energy below the valence band are “filled” with electrons, so it is only the valence and conduction band that is most important.

Fig. 1

Each material has a “fermi level” (the extent to which the electrons fill the bands at absolute zero) and the energy level to which the bands are filled will give information about the material.  The question then becomes, if each element in the periodic table has discrete bands of energy that electrons could POTENTIALLY live in , are these bands occupied or unoccupied by electrons? And what does this have to do about the classification of materials?

Using the examples of insulators, conductors and semiconductors, we can see how the band structures will help us classify these materials as such (see fig. 2).

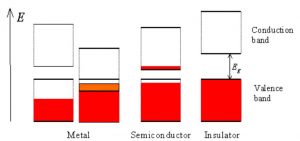
Fig. 2

Insulators: For insulating materials, the fermi level lies between the valence and conduction band. This means that the entire valence band is filled, and therefore cannot conduct electricity. You can compare this to a busy highway that is filled with cars transporting electricity. There’s so much traffic that none of the cars can move, and therefore no electricity is moving as well.

Conductors: Conducting materials have a fermi level that lies halfway between a band itself. This is called a “half-filled band”. Using the same analogy before, this is as if the cars transporting electricity are on a highway with plenty of room to travel, thus electricity is being transported efficiently.

Semi-conductors: Similar to insulators, the fermi level for semi-conductors lies in between the valence and conductance band. However, in contrast to insulating materials, the distance between the valence and conductance band is smaller. This means that electrons with a high enough energy can “jump” into the conductance band, and electricity can flow. You can think of this as if on a very busy highway, cars with high enough occupancy can enter the HOV lane, and move unencumbered by traffic.

Citations:

(1) Zeeghbroeck, B. Van. “Chapter 2: Semiconductor Fundamentals.” Principles of Semiconductor Devices, 2011, ecee.colorado.edu/~bart/book/book/chapter2/ch2_3.htm.

(2) Singh, Jasprit. Electronic and Optoelectronic Properties of Semiconductor Structures. Cambridge University Press, 2003.

(3) Kittel, Charles. Introduction to Solid State Physics (8th Edition). John Wiley & Sons, Inc., 2005.