Author Archives: Steve
Tutorial #2 Problems
- Rank the following functions by order of growth. That is, order them so that f1 ∈ O(f2), f2 ∈ O(f3), etc. Make sure to indicate whether or not fi ∈ Θ(fi+1). For instance you could use the notation O(n) ⊂ O(n^2) = O(2n^2) ⊂ O(n^4)...
n3 – n √ n
n! log (log n) 1.01n √ n log n
17 4913n289 32n-17 1.011.01n √ n
3n nn n18/17 n log17 n 32n n3 + log n - Prove that for each fixed value of k > 0, 1k + 2k + … + (t-1)k + tk ∈ Θ(tk+1). Hint: do not use induction. Instead, treat k as a constant, and do O and Ω separately. (Remember that for Ω bounds, it is legal to drop positive terms and reduce the size of positive terms, since you can guarantee that the resulting function is still a lower bound on the original.)
- Analyze the running time of the following algorithm as a function of n, assuming that each arithmetic operation takes constant time. Use O, Ω or Θ notation as appropriate to express your result as simply and as precisely as possible. Give an informal argument (not necessarily a full proof) to support your answer. (It may help to think about the “measure of progress” approach the book used to analyze the while loop in the Gale-Shapley Algorithm.)
Algorithm Strange(n) sum ← 0 while (n > 3) do sum ← sum + n if (n is even) then n ← n / 2 else n ← n + 3 endif return sum
Slides #5: Graphs Intro
Today’s playing with graphs handout (in PDF).
We had reading questions on graphs as well:
- 8AM: “If we start from the top node and always visit left children before right children where there’s a choice, which one would visit the node with the first (leftmost) digit of your student number on it first, depth-first search or breadth-first search?” In:
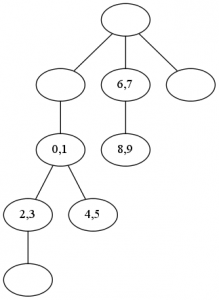
- 11AM: “A tree is a particular type of graph. If we consider the node numbered by the first (leftmost) digit of your student ID the root, is this graph a tree?” In:
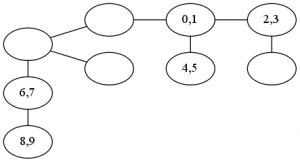
Read Before 2015/01/19 Class
- Section 3.3
- Section 3.4
(If you want to get ahead, 3.5 and 3.6 are coming up, and then we’ll move on to Chapter 4. We may follow the advice on page xx regarding skipping 4.3 and 4.7-4.9, but I have not yet decided. I may also introduce one extra reading before Chapter 4, but we’d still get to Ch 4 before long!)
Read Before 2015/01/16 Class
- Section 3.1 and 3.2
Much of these sections will be review, but there should be some fun new ideas in graphs and graph algorithms!
Assignment #2
PDF document: Assignment #2
Due Monday 2015/01/19 at 5PM in our submission box (#32).
- Use the assignment cover page.
- Read the academic conduct guidelines or expect horrendous consequences for you.
- Please work with a partner; you’ll learn more, and we’ll spend less time on marking and more on making the course awesome.
Protected: Assignment #1 Sample Solution
Slides #4
- Asymptotic analysis and orders of growth problems handout.
- Some notes on Little-ο and Little-ω.
Our reading question on this set was essentially:
Consider the following problem: Given a list of n integers, determine whether any subset of ____ of the integers sum to 42.
Now, with a brute force solution, does this take polynomial or exponential time?
The blank in that was filled with “three” for one section and with “any size” for the other section. For “three”, the answer is polynomial time because we can construct a triply nested loop to produce all sets of size three and check each one in constant time. (For “four”, it would be a quadruply nested loop.) For “any size”, the answer is exponential because there are 2n subsets of n elements.
Read Before 2015/01/14 Class
Review Monday’s reading.
Tutorial #1 Problems
Problems for tutorial #1
- Consider the Coop Student/Company Matching Problem: n students apply for jobs at m companies, where company i is looking for ni COOP students. There are at least enough students to fill all of the positions (and there may be too many). Every student has a ranking of companies in order of preference, and each company has a ranking of students in order of preference. An assignment of students to companies is stable if neither of the following situations arises:
- There are two students s and s' and a company c such that s is assigned to c, s' is unemployed, and c prefers s' to s.
- There are two students s and s', and companies c and c', such that s is assigned to c, s' is assigned to c', s prefers c' to c, and c'prefers s to s' (the usual type of instability).
Describe an efficient algorithm that will produce a stable assignment of students to companies, first using a reduction and the Gale-Shapley Algorithm, and then by modifying the G-S Algorithm so that it works directly on this problem.
- Prove or disprove each of the following two statements. That is, either prove that the statement is true, or give an example to show that it is false. Hint: exactly one of the statements is true.
- In every instance of the Stable Matching Problem, there is a stable matching containing a pair (w, m) such that w is ranked first on the preference list of m and m is ranked first on the preference list of w.
- Consider an instance of the Stable Matching Problem in which there exists a man m and a woman w such that m is ranked first on the preference list of w and w is ranked first on the preference list of m. Then in every stable matching S for this instance, the pair (w, m) belongs to S.
- (Induction review) Suppose you begin with a pile of n stones, and split this pile into n piles of one stone each by successively splitting a pile of stones into two smaller piles. Each time you split a pile you multiply the number of stones in each of the two smaller piles you form, so that if these piles have r and s stones in them, respectively, you compute rs. Show that no matter how you split the pile, the sum of the products computed at each step equals n(n-1)/2. Here is an example that shows how the computation proceeds:
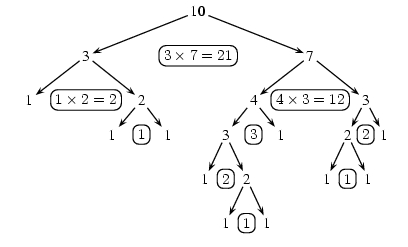
The sum is 21+2+12+1+3+2+2+1+1 = 45, which is indeed 10 * 9 / 2.