[previous] [next]
Problem
The length of time X, needed by students in a particular course to complete a 1 hour exam is a random variable with PDF given by
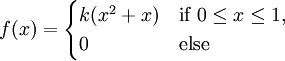
For the random variable X,
- Find the value k that makes f(x) a probability density function (PDF)
- Find the cumulative distribution function (CDF)
- Graph the PDF and the CDF
- Use the CDF to find
- Pr(X ≤ 0)
- Pr(X ≤ 1)
- Pr(X ≤ 2)
- find the probability that that a randomly selected student will finish the exam in less than half an hour
- Find the mean time needed to complete a 1 hour exam
- Find the variance and standard deviation of X
Solution
Part 1
The given PDF must integrate to 1. Thus, we calculate
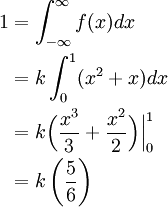
Therefore, k = 6/5.
Part 2
The CDF, F(x), is area function of the PDF, obtained by integrating the PDF from negative infinity to an arbitrary value x.
If x is in the interval (-∞, 0), then
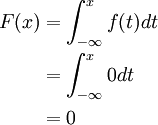
If x is in the interval [0, 1], then
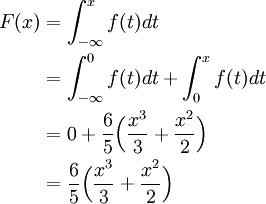
If x is in the interval (1, ∞) then

Note that the PDF f is equal to zero for x > 1. The CDF is therefore given by
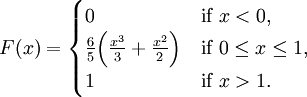
Part 3
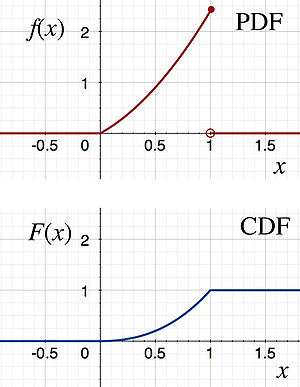
The PDF and CDF of X are shown below.
Part 4
These probabilities can be calculated using the CDF:
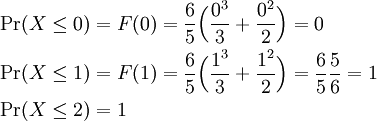
Note that we could have evaluated these probabilities by using the PDF only, integrating the PDF over the desired event.
Part 5
The probability that a student will complete the exam in less than half an hour is Pr(X < 0.5). Note that since Pr(X = 0.5) = 0, since X is a continuous random variable, we an equivalently calculate Pr(x ≤ 0.5). This is now precisely F(0.5):
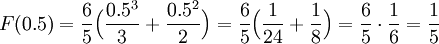
Part 6
The mean time to complete a 1 hour exam is the expected value of the random variable X. Consequently, we calculate
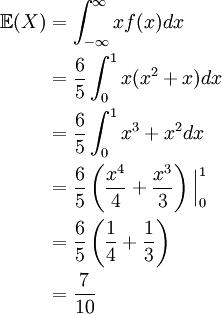
Part 7
To find the variance of X, we use our alternate formula to calculate
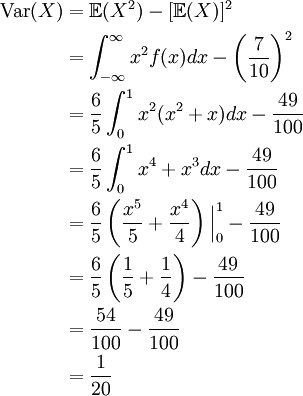
Finally, we see that the standard deviation of X is
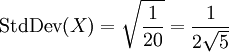
[previous] [next]