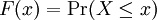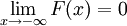[previous] [next]
We previously defined a continuous random variable to be one where the values the random variable are given by a continuum of values. For example, we can define a continuous random variable that can take on any value in the interval [1,2].
To be more precise, we recall the definition of a cumulative distribution function (CDF) for a random variable that was introduced in the previous lesson on discrete random variables.
| Definition: The Cumulative Distribution Function |
|---|
| The cumulative distribution function for a random variable X, denoted by F(x), is the probability that X assumes a value less than or equal to x:
The cumulative distribution function has the following properties:
Additionally, for continuous random variables, F(x) is a continuous function. |
From this, we can define a continuous random variable to be any random variable X whose CDF is a continuous function. Notice that this is in contrast to the case of discrete random variables where the corresponding CDF is always a discontinuous step-function.
Comparison to the Discrete Case
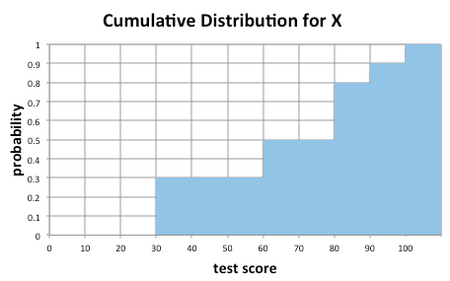
Recall the cumulative distribution function we had for the test scores example in the previous lesson. The cumulative distribution function was graphed at the end of the example.
Observe that
- from 0 to 30, F is constant because there are no test scores before 30
- from 30 to 60, F is constant because there are no scores between 30 and 60.
The graph of F "increases in steps" at 30, 60, 80, 90, and 100. CDFs for discrete random variables are always step functions. A discrete random variable cannot assume a continuum of values; thus, its CDF can only increase at a finite or countably infinite set of points.
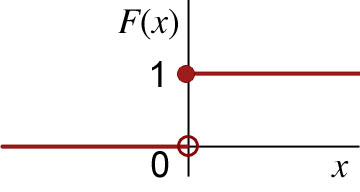
For another example, consider the function whose graph is given below.
This function cannot represent a CDF for a continuous random variable because the function F is not continuous for all values of x. However, F could represent a cumulative distribution function for a discrete random variable since it satisfies our definition from the previous lesson on discrete random variables.
[previous] [next]