[previous] [next]
Question
Let f(x) = k(3x2 + 1).
- Find the value of k that makes the given function a PDF on the interval 0 ≤ x ≤ 2.
- Let X be a continuous random variable whose PDF is f(x). Compute the probability that X is between 1 and 2.
- Find the distribution function of X.
- Find the probability that X is exactly equal to 1.
Solution
Part 1)
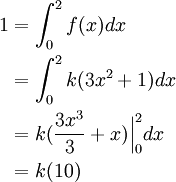
Therefore, k = 1/10.
Notice that f(x) ≥ 0 for all x. Also notice that we can rewrite this PDF in the obvious way so that it is defined for all real numbers:
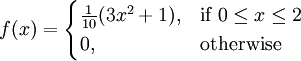
Part 2)
Using our value for k from Part 1:
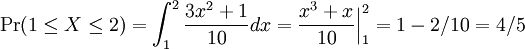
Therefore, Pr(1 ≤ X ≤ 2) is 4/5.
Part 3)
Using the Fundamental Theorem of Calculus, the CDF of X at x in [0,2] is
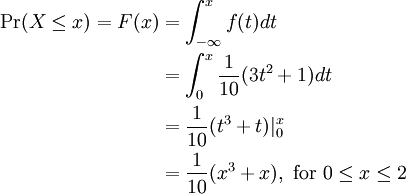
We can also easily verify that F(x) = 0 for all x < 0 and that F(x) = 1 for all x > 2.
Part 4)
Since X is a continuous random variable, we immediately know that the probability that it equals any one particular value must be zero. More directly, we compute
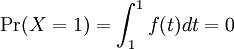
[previous] [next]
