Votes & Seats under the Alternative Vote

In this post, I consider the proportionality of the Alternative Vote (AV), that is, the degree to which AV produces a 1:1 ratio between parties’ vote shares and their seat shares. (AV is the electoral system that is purportedly the Liberal’s favoured alternative to replace Canada’s first-past-the-post electoral system (FPTP).)

By using data from Australian federal elections as well as state elections in Australia’s five mainland states, we can see how AV tends to perform in six different polities.* Moreover, because these jurisdictions all employed FPTP at some point in time, we can also consider whether the shift to AV altered the votes-seats proportionality of Australian elections. This should give us some idea of what to expect should Canada adopt AV.

A priori, we should not expect AV to be any more or less proportional than FPTP. The reason is that both system tend to employ single-member districts. The number of seats per district—what political scientists call the district magnitude—constrains the proportionality of an electoral system quite independently of the formula that is used to translate votes into seats. The higher the district magnitude, the more closely the division of seats among parties can approximate the distribution of vote shares among parties. This improves the votes-seats proportionality of the electoral system. Conversely, votes-seats proportionality that is achievable declines as the district magnitude moves to 1.

Understand that the impact of district magnitude on votes-seats proportionality operates at the district-level. It’s quite possible for an electoral system based on single-member districts to be proportional in aggregate even as it is highly disproportional in every district. Imagine a polity with three parties (A, B, C) competing in FPTP elections in three single-member districts (1,2 3). Assume that party A wins 34% of the vote in district 1 versus 33% for parties B and C, respectively. Similarly, B wins district 2, and C wins district 3, on identical divisions of the vote, that is, 34% – 33% – 33%. The result is a high degree of disproportionality within each district (the party winning 34% of the vote obtaining 100% of the district’s seats) but perfect proportionality in the aggregate, each party winning 1/3 of the seats on 1/3 of the vote.

Of course, district-level disproportionality need not (and often does not) cancel out across districts; it may well be compounded. Indeed, in the past governing parties would intentionally gerrymander and malapportion districts to ensure that disproportionality compounded across districts: district boundaries were drawn to ensure that the government won the vast majority of seats by razor-thin margins whilst the opposition’s votes were concentrated in a few districts which it would win by massive margins. But disproportionality can also be compounded across districts because of how voters cast their votes. In closely contested multi-party elections supporters of 3^rd place parties tend to defect to one of the two leading parties in their district. In the aggregate this results in the top-two vote-winning parties obtaining seat shares in excess of their votes and 3^rd+ place parties obtaining seat shares below their vote shares.

Votes & Seats in Canada under FPTP

Figure 1. (right-click to enlarge)

This pattern is visible in Figure 1, which shows the relationship between vote- and seat-shares at Canadian general elections since 1949. A perfectly proportional electoral system would allocate seat shares to parties such that all outcomes fell on the dashed 45° line, indicating a 1:1 ratio between parties’ vote-shares and seat-shares. Instead, what we see is that the red and blue dots (representing the Liberals and Conservatives, respectively) are consistently above the 45° line whenever their vote-shares exceed 35 percent. Correspondingly (because elections are zero-sum), parties with vote-shares below 35% consistently fall below the 45° line. The few exceptions to this rule are regional parties (notably the Bloc Quebecois and Reform).

We can describe the Canadian data more precisely by regressing parties’ seat-shares (S%_it) on their vote-shares (V%_it) and a set of election-year fixed effects (Y_t):

S%_it = a + bV%_it + dY_t + u_it [1]

Disproportionality is signalled by b ≠ 1. Estimating Eq. 1 via OLS yields

b = 1.28 (.03)

Adj. R² = .88  RMSE = 7.20

N Obs = 119  N Clusters = 22

Huber-White SE clustered by election in parentheses

No surprise here: Canada’s FPTP electoral system is quite disproportional.

It is interesting and informative to modify Eq. 1 to include the square of parties’ vote shares.

S%_it = a + b₁V%_it + b₂V²%_it + dY_t + u_it [1b]

This specification allows for nonlinear and increasing returns to votes. Estimating Eq. 1b via OLS yields:

b₁ = .06 (.11)  b₂ = .028 (.002)

Adj. R² = .95  RMSE = 4.74

N Obs = 119  N Clusters = 22

Huber-White SE clustered by election in parentheses

These results tell us that the marginal effect of votes on seats in Canada increases as the party’s vote-share increases. To be precise, a party’s seat-share increases by .06 + .028V%_it for every 1% of the vote the party wins. So the larger a party’s vote-share, the greater the rate at which it translates votes into seats. In fact, one can deduce that the Canadian system’s “break-even” point is 33.6% of the vote; every 1 percent of the vote won after this point returns greater than 1 percent of seats.

Votes & Seats in Australia

The Canadian data provide a context within which to consider the proportionality of Australia’s AV electoral system. Figure 2 below shows vote shares and seat shares at Australian federal and state elections since 1890. The colour coding in Figure 2 varies by electoral system. So one sees the relationship between votes and seats under not just FPTP and AV but also the Contingent Vote (CV) in Queensland, and STV and 2-round plurality in NSW.

Figure 2. (right-click to enlarge)

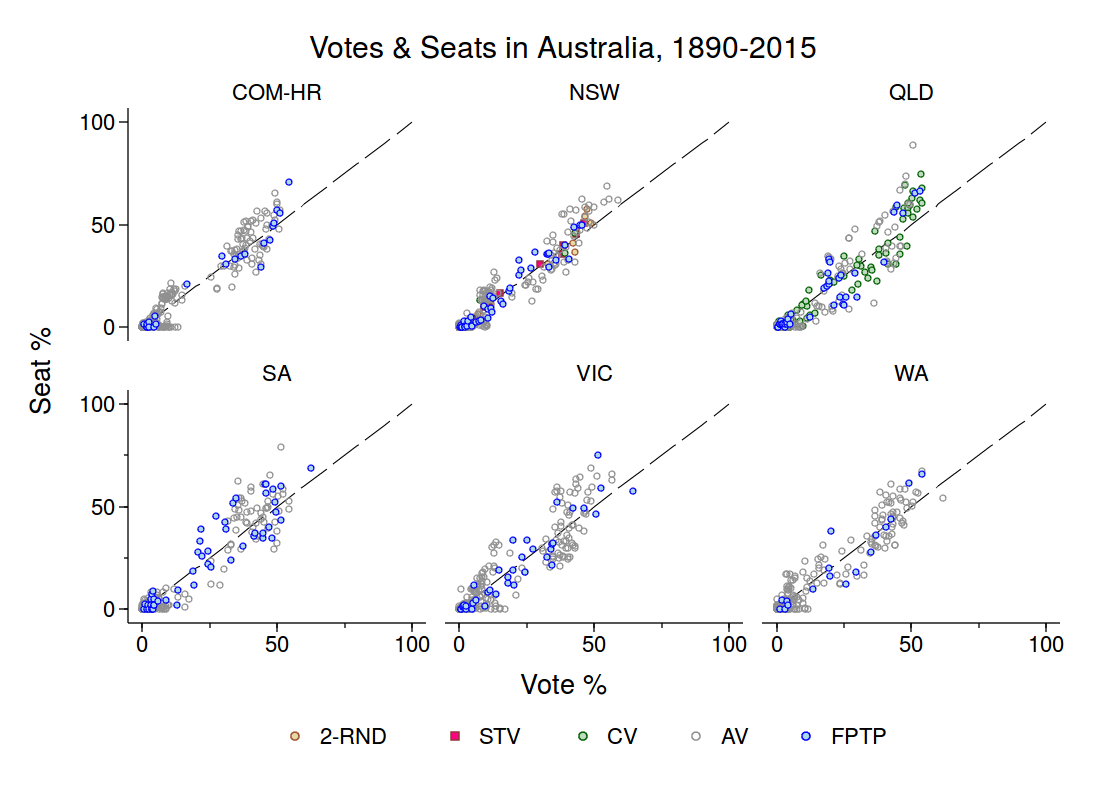
I find three things noteworthy about Figure 2.

1. Australian elections are characterized by disproportionality. Observe that parties that obtain 35-40+% of the vote tend to have seat-shares that fall above the 45° line that marks perfect proportionality.
2. Disproportionality at Australian elections does not appear as severe as it is at Canadian elections. It’s really only in Queensland that the return to votes is visibly non-linear and increasing.
3. It’s not obvious on these data that elections under FPTP were significantly more disproportional than those held under AV.

Of course, these are just my impressions of the visual data; it’s worth exploring the data more systematically. Now, in assessing the votes-seats proportionality of Australian elections we want to:

• account for the fact that some of these elections employed multi-member districts;
• allow the relationship between votes and seats to vary by state; and
• identify the impact on proportionality of shifting from FPTP to AV.

I do all this by: i) controlling for the average district magnitude at election t in state j (M_tj); ii) adding state fixed-effects (STATE_j) to the model and interacting these state fixed-effects with parties’ vote-shares (V%_ijt); and iii) including a dummy variable, AV_jt , that equals 1 when AV is used and 0 when FPTP is used. (Elections that employed other electoral systems are dropped.) The model is

S%_iit = a + d₁M_tj + d₂Y_t + d₃STATE_j + b₁V%_ijt + b₂(V%_ijt * STATE_j) [2]

+ b₃(V%_ijt * AV_jt) + b₄(V%_ijt * STATE_j * AV_jt) + e_ijt.

The quantity of interest here remains the marginal effect of votes on seats, that is, the rate at which vote-shares are translated into seat-shares. The interactions between V%_ijt and STATE_j and AV_jt in Eq 2 allow this rate to vary by state and by electoral system.

Figure 3. (right-click to enlarge)

Figure 3 shows the marginal effect of votes on seats for each state under FPTP and AV. The circles represent the point estimates, and the bars show the 90% confidence intervals surrounding these estimates. So what Figure 3 tells us, for example, is that for every 1% of the vote a party won at elections to the Commonwealth’s House of Representatives (COM-HR) it obtained about 1.08% of the assembly’s seats on average. In other words, Australian federal elections are mildly disproportional. Furthermore, the proximity of the blue and gray dots tells us that the relationship between votes and seats at Commonwealth elections was unaffected by the shift from FPTP to AV.

In the main, the same remarks can be extended to all five mainland states. Only Victorian elections – held under FPTP no less – might, maybe have been proportional. In no state did AV make elections reliably more proportional – though it came close to doing so in Western Australia. Of course, Australian elections were never as disproportional as Canadian federal elections; only elections in Queensland come close – and that probably has a lot more to do with how the Nicklin and Bjelke-Petersen governments malapportioned and gerrymandered electoral districts than the electoral system itself.

To better isolate any causal effect of the electoral system on votes-seats disproportionality, I estimated Eq. 2 again, but with the data limited to just the very last elections held under FPTP and the elections held immediately thereafter on the adoption of AV. This eliminated NSW from the analysis (because NSW experimented with several electoral systems between abandoning FPTP and adopting AV). District magnitudes did not vary within states at these transitional elections, so there was also no need to control for the average district magnitude. The model was then:

S%_iit = a + d₁STATE_j + b₁V%_ijt + b₂(V%_ijt * AV_jt) + e_ijt [2b]

Under this model, the marginal effect of vote-shares on seat-shares under FPTP is given by b₁, whilst under AV it’s given by b₁ + b₂. Estimating Eq. 2 via OLS returned 

b₁ = 1.10 (.04)  b₂ = -.04 (.08)

Adj. R² = .88  RMSE = 8.51

N Obs = 47  N Clusters = 10

Huber-White SE clustered by election in parentheses

Thus the ratio of vote- to seat-shares was 1:1.10 under FPTP and declined to 1:1.06 under AV – BUT this decline is not statistically significant (not by a long-shot). In other words, we can’t rule out that the shift to AV made no difference whatsoever.

Finally, I estimated an Australian analogue to Eq 1b. containing parties’ vote shares and their squared vote shares – but only using data from AV elections:

S%_iit = a + d₁Y_t + d₂STATE_j + b₁V%_ijt + b₂V²%_ijt + e_ijt [3]

Estimating Eq. 3 via OLS yields:

b₁ = .89 (.06)  b₂ = .004 (.0016)

Adj. R² = .88  RMSE = 6.56

N Obs = 1209  N Clusters = 180

Huber-White SE clustered by election in parentheses

These results indicate that AV also generates nonlinear and increasing returns to votes, although not nearly so sharply as in Canada.  The “break-even” point under AV is also lower at 27.5%

Discussion

There’s no reason to expect AV to be any more proportional an electoral system than FPTP. This is because the proportionality of the electoral system is tightly constrained by the number of seats per district, and both AV and FPTP are typically used with single-member districts.

The data from Australian state and federal elections are consistent with this theoretical expectation. Australian elections do not produce the level of disproportionality that is observed in Canadian elections – but this probably has little to do with Australia’s AV electoral system because the adoption of AV in favour of FPTP in Australia had no discernible impact on electoral disproportionality.

What does this mean for electoral reform in Canada? These data suggest that we should not expect the disproportionality of the Canadian electoral system to change appreciably were the Government to choose AV to replace FPTP. Disproportionality systematically favours larger parties over smaller parties, and to that extent the Conservatives should not be particularly apprehensive of a transition to AV. As I observed previously, a shift to AV could position the Conservatives as a right-wing version of the ALP – not often in government, but dominant on their part of the political spectrum. Correspondingly, the NDP and the Greens should not expect an AV electoral system on its own to improve the efficiency with which these two parties translate votes into seats.

In my next post I’ll explore another aspect of AV – it’s volatility.

---

* A big thanks to my colleague, Campbell Sharman for furnishing me with these data.