Reducing Test Anxiety in Gifted and Non-Gifted Adolescent Mathematics Students:
A Mixed Methods Approach
Dana E. K. Bjornson (neé Allingham)
The University of British Columbia
April 10, 2015.
Introduction
Imagine this scenario: ten minutes ago, everything was fine. You had a great sleep, an even better breakfast, and now you are about to start your work for the day. Suddenly, you realize that your heart is starting to race, your palms are starting to sweat, and the simple task of writing your name on a piece of paper is causing your neck muscles to stiffen. What you may or may not realize is that your body is responding to your brain’s activation of its “fight or flight” mechanism. Now, this response would be appropriate and even beneficial if your job entailed running away from bears in a national park; however, in this scenario, imagine that you are sitting down to write a secondary-school mathematics test. While the math test is hardly about to devour you as if it were a hungry bear, your body is physiologically responding to the perceived threat of danger, and your physical symptoms are as real as if you were responding to the sudden appearance of a bear in front of you. In this scenario, you are experiencing an anxiety attack.
Characteristics of Anxiety
The central theme to all types of anxiety is worry. Worry is a cognitive process that is characterized by having repetitive, negative thoughts of a perceived threat (Huberty, 2012, p. 30). Table 1 in the Appendix lists typical characteristics of anxiety that can manifest themselves cognitively, behaviourally, and/or physiologically. Although none of these characteristics is particularly desirable, characteristics such as impaired concentration and defective memory, problem-solving difficulties, and cognitive dysfunctions are extremely harmful to one’s achieving one’s potent when one is about to write any sort of a test! Mathematics anxiety, specifically, can be described as “anxiety that interferes with one’s ability to manipulate numbers and problem solve in mathematic related situations” (Richardson & Suinn, 1972). Such anxiety results in a student’s performing below his or her potential, and therefore compromises the reliability of the test.
Anxiety and the Gifted Learner
Some characteristics of gifted learners make them more prone to experiencing higher rates of mathematics anxiety, whereas other ‘gifted’ characteristics tend to reduce or prohibit signs of anxiety. Although gifted learners typically exhibit positive traits such as high levels of intelligence, mental agility, creativity, high recognition vocabulary, and unflappable inquisitiveness, they can also possess negative traits such as perfectionism, low self-confidence, frequent instances of frustration, and a lack of perseverance (Distin, 2006, p. 22-30). How, then, does ‘math anxiety’ specifically affect gifted learners in a test setting?
Relevance of this study
Having been a math educator since 1997, I find this topic very compelling. I have personally witnessed students experience test anxiety at every level of the spectrum. At its most innocuous, anxiety can make a student perspire before taking a test; at its worst, anxiety can psychologically paralyze students to the point of rendering them unable to attend school for months or contributing to their contemplating suicide. Although much research has been done on anxiety in general, very little has been done to investigate anti-anxiety strategies specific to a secondary mathematics classroom. It is my hope that this study will keep the conversation about and the investigation of math anxiety moving in a direction that will not only benefit students as they negotiate their math classes, but also as they transition through to adulthood as mathematically literate citizens.
Problem Statement
Purpose
The purpose of this study is to examine how “gifted” and “non-gifted” mathematics students respond to anxiety-reducing techniques within the context of their Mathematics 10 course.
Research Questions
- What are the causes or triggers specific to math anxiety in Grade 10 students?
- How does exposure to anxiety-reducing techniques affect perceived anxiety levels immediately before testing has occurred?
- Are there differences in how anxiety-reducing techniques affect the levels of math anxiety in “gifted” and “non-gifted” students?
Critical Review of Literature
Introduction
This review of literature includes both primary and secondary sources. There are four articles from scholarly journals, two of which were based on the results of the authors’ own primary research. This review also includes three research reports and two books pertaining to anxiety and to the gifted learner. This review will be organized under two major categories: mathematics anxiety and the gifted learner.
Mathematics Anxiety
Conducting further research in the area of mathematics anxiety could potentially benefit all levels of education and society. One study has estimated that the numbers of students who experience mathematics anxiety is over one-third (Richardson & Suinn, 1972); on the other hand, two other studies (conducted by Cizek & Burg in 2006 and Huberty in 2009) have estimated that “test anxiety,” in general, affects somewhere between 25% and 40% of secondary students (as cited in Salend, 2011). Multiple researchers also agree that math anxiety leads to avoidance of subjects involving mathematics, thereby limiting potential career paths for students who might otherwise succeed in those careers (Richardson & Suinn, 1970; Hembree, 1990; Ashcraft, 2002; Chernoff & Stone, 2014). Furthermore, in 1989, William Bush’s study showed that elementary teachers suffering with their own math anxiety favoured teaching algorithms and skills as opposed to adhering to best practice guidelines that also emphasize concepts. Studying mathematics with such teachers, students are then more susceptible to developing a lack of understanding as to why the algorithms are in place, and thus has the potential to create new generations of math-anxious students (as cited in Chernoff & Stone, 2014). Not surprisingly, elementary teachers exhibited the highest degree of mathematics test anxiety compared to all other groups in a meta-analysis process of synthesizing 151 previous studies (Hembree, 1990). It is clear, then, that math anxiety exists; so what can mathematics researchers do to alleviate its effects and reduce its incidence?
Anxiety and the Gifted Learner
In 2013, I was in attendance at a public meeting in my children’s school district in Langford, British Columbia. The meeting was intended to collect public feedback on the structuring of a new high school’s being built in the district. Since I am a teacher in the gifted education program in Victoria, I asked the superintendent if there were any plans to create a similar program in the new secondary school. He promptly replied that, when this idea was last discussed, the teachers in his District were against such a plan, as they “didn’t want all of their smart kids to leave their classrooms.” Sadly, this narrow understanding of the needs of the gifted learner is prevalent among teachers if they have not had some sort of professional training in the delivery of gifted education. Prior to training in gifted education, one group of teachers described gifted learners as “bright, confident, and fortunate,” whereas after the training, the same teachers used such terms as “vulnerable, complex, and needy” (Distin, 2006, p. 118). How “needy” and “vulnerable” are such students? In a recent study of gifted students, researchers found a correlation of 0.56 between anxiety and depression in gifted high school students (Yazid, Bakar & Ishak, 2014). In other words, there is some correlation between test anxiety and above-average potential in mathematics.
Not all research agrees, however, that the gifted are more vulnerable than their non-gifted counterparts. In 1999, Zeidner and Schleyer studied 772 gifted and 716 regular Israeli students in Grades 4 to 9. They found that the gifted students who were integrated into regular classrooms self-reported lower levels of academic anxiety, a finding which may be explained by their high academic self-efficacy nature. The Zeidner & Schleyer study, however, focusses on a younger student as opposed to an older student, that is, a student who may be facing academic challenges for the first time. In my own experience with gifted students, they will sometimes report, “I never had to work for my grades, but that, now that the material is harder, I don’t know how to study.” In secondary school mathematics, the working memory must be accessed in most processes, since the problems almost always require multiple steps. When multiple steps are involved, working memory is required, and test anxiety increases in those who are predisposed to mathematics anxiety (Ashcraft & Krause, 2007). Thus, for students who are experiencing mathematical challenges for the first time, frustration and avoidance of the subject are likely to occur. This sense of frustration may also be coupled with a lack of perseverance since gifted learners are not accustomed to having to “work” for their comprehension of a concept or process (Distin, 2006, p. 36).
Indeed, many researchers report high levels of frustration for gifted learners due to setting unrealistic standards (Zeidner & Schleyer, 1999; Distin, 2006, p.34; Yazid et al., 2014). Compounding this effect are learning environments in which gifted students are segregated into separated programs for purely gifted learners. Zeidner & Schleyer found that these students’ self-perception of their intellectual ability (their self-esteem) was much lower than their non-segregated counterparts. Zeidner and Schleyer concluded that the social comparison in a collective of highly able individuals could lead to the gifted learner’s to feeling inadequate, frustrated, and increasingly anxious. Other studies have shown that unrealistic expectations (real or perceived) of parents and educators can also add fuel to the anxiety fire, a phenomenon which could be intensified should the students be in a specialized program for gifted learners (as cited in Yazid et al., 2014).
Conclusion
Few will argue that the demands on classroom teachers in all secondary subjects have increased over the past four decades. As educational research continues to dig more deeply and more broadly into existing and trending topics, and as access to this new research has become accessible to anyone with an internet connection, educators are assuming responsibilities beyond simply teaching their subject matter. Moreover, with the rampant use of state-sponsored standardized testing, teachers are not only losing valuable class time to test preparation, they are also being required to cover a vast number of state-mandated learning outcomes. These “high stakes” tests (that in British Columbia are mostly administered at the Grade 10 level) are also contributing to heightened anxiety throughout the student population, gifted or otherwise (Salend, 2011).
Not only will this study target the population of students who are facing high stakes, government exams for the first time, it will also provide evidence that justifies and supports teachers’ decisions to utilize class time to coach their students through their test anxiety that may exist in the math classroom. As Grade 10 gifted learners may be experiencing genuine academic challenges for the first time, and since they have a wide array of characteristics unique to their cohort, this research may shed more light on the anti-anxiety techniques that work best for them as a subset of the secondary school population.
Research Method
Description of research methods
For my study, I intend to do a “mixed methods” approach that provides opportunity to maximize the benefits and counter the drawbacks of both the qualitative and quantitative research processes. Utilising a quasi-experimental, non-equivalent control group design field experiment that monitors students’ anxiety levels using a survey, I will also have a subset of the students undergo a series of reflections and structured interviews. As the quantitative surveys and the qualitative reflections will be conducted concurrently throughout the semester, I will apply the triangulation mixed methods design, also known as QUAN-QUAL, so that statistically significant findings are validated by students’ comments.
Participants
Description of participants. Four classes will be utilized for this study: two gifted and two regular, academic Mathematics 10 classes. Two of the classes will constitute the experimental group, and two of the classes will constitute the control group. The control group, consisting of two classes (one gifted and one regular), will be taught by other teachers; however, I will teach the experiment group. For qualitative component, three students who have a “moderate” amount mathematics anxiety will be recruited from each experimental class.
Rationale for selection and exclusion of participants. As I mentioned in the Review of Literature, studies involving anxiety in gifted learners have focussed for the most part on intermediate and middle school years, not on Grade 10. Due to “high stakes” testing starting in Grade 10 in British Columbia, this grade represents a group in which a significantly higher degree of stress is introduced into students’ lives. Compounding this negative effect, researchers report that mathematics anxiety tends to peak in Grades 9 and 10 (Hembree, 1990). Students who are mathematically challenged tend to take Applied and Workplace (A & W) mathematics, and therefore the study’s focus on the students in the academic mathematics course, Foundations and Pre-Calculus (FPC) Mathematics, will reduce threats to validity resulting from statistical regression. In the same vein, students who are tested with extremely high or low levels of pre-existing mathematics anxiety will not be utilized in the case study. These students will be selected based on a “moderate” anxiety ranking on an initial, pre-test survey and in light of their post-unit test responses to the first reflection activity. I will look for students who provide reflections in a thorough and seemingly honest manner. Finally, I wish to exclude students from the case study who are repeating the course, so that all participants in this component of the study have the same level of mathematics experience prior to entering the study.
Recruitment. Utilising my own classes for the experimental group will make some of the recruitment very simple. The challenge will be to recruit two additional classes to serve as controls: one gifted and one regular. I will be contacting other Mathematics 10 teachers from across the district to secure these control groups for two reasons. Typically, my school only has one gifted Math 10 class per year; however, across town there is another district gifted education program. Secondly, in order to reduce the effect of treatment diffusion, having the control groups located outside of my school would likely eliminate that effect. Prior to choosing these control groups, I would need to determine what strategies and policies the teacher(s) already utilize. Ultimately, I would like to find colleagues who teach mathematics with more traditional, potentially anxiety-causing techniques, such as timed tests. It is possible that I may have to recruit outside of my school district, however, in order to satisfy this condition.
Ethical issues. Parental permission will unquestionably be required for students whom I wish to participate in the study. It is feasible that a student with extreme anxiety issues would be uncomfortable or potentially unable to participate. Ultimately, participation in my study would be voluntary and names would be held in confidence, with the best interests of the students always being held paramount. Documents will be held in strict confidence, and only data pertaining to overall results of the study will be released to the public. No data or instruments will be destroyed for five years, during which these will be securely stored in locked filing cabinets and on a password-controlled computer. General results of the study, however, will disseminated to student participants, their parents, and their teachers upon conclusion of the study.
Instruments
Quantitative component. In the first week of class, I will administer a cross-sectional survey that takes a quick snapshot of the students’ self-perceived mathematics anxiety levels (Appendix, Figure 1). The survey consists of some basic demographic information, such as name, age, and whether or not this is the first time taking the course. It then proceeds to use a 5-point Likert scale from “Extremely” to “Not at all” that asks students to rank ten statements pertaining to their emotional and distress levels that they tend to experience during math tests and in completing practice work. Since this survey has been adapted from the Westside Anxiety Test, its statements are specific to mathematics anxiety, as opposed to test anxiety in general (Driscoll, 2007). Each response is given a point value; and survey-takers’ responses will be averaged to a score out of five in each case. Using Westside’s rating system, I will be able to determine the anxiety levels of my students quickly and effectively (Appendix, Table 2). A quick search in UBC’s Commons listed numerous studies that have used this anxiety scale to quantify anxiety levels resulting from testing, thus providing me with confidence levels pertaining to the validity of this survey. The survey will be administered using the CPS Student Response System, which will allow for students to enter in their responses into a “clicker” without fear of their neighbours’ looking at their self-assessment. At the end of the course, I will administer this identical survey to compare where they are presently in their mathematics anxiety with their anxiety level before taking the course.
The second component to the quantitative piece will be the pre-math test survey, entitled “Pre-Math Test Check-in.” This is a self-developed, 4-point Likert Scale that allows students to determine graphically which statement most describes how they are feeling immediately before they write each unit test in the course. Instead of utilizing words to describe their feelings, I have chosen to utilize an arrow system that students can use to judge reliably their frame of mind both quickly and effectively (Appendix, Figure 2). Students will read seven statements, one at a time. The leftmost statements represent the statements with which a typically calm and prepared student would identify, whereas the rightmost statements would typical of students who exhibit signs of mathematics anxiety. Students can also gauge to what extent they identify with a side by choosing either the single arrow, “<” or the double arrow, “<<”.
Qualitative Component. The day after each unit test has been written, each student will complete a very short reflection sheet that completes the following statements:
- I did well on yesterday’s test because…
- I struggled on yesterday’s test because…
- The things I can do to be successful on future tests are …
The motivation behind this reflection piece is to promote what is referred to as “Attribution Training.” Some students will enter testing situations “knowing they are going to fail,” even though they have prepared for the assessment. Attribution training helps these students positively and correctly attribute their achievements to the correct cause, thereby reducing anxious feelings prior to testing (Salend, 2011).
The six students who will be part of the ethnographical case study will be required to participate in three structured, audio-recorded interviews, at the beginning, middle, and end of the course. These interviews will each serve different purposes. The initial interview will let me find out about their “math history” and what triggers them personally to experience mathematics anxiety. During this interview, I will help each participant craft a “game plan” for the course and, most importantly, during this interview, I will establish a rapport with the student. The mid-semester interview will serve as a check-in: I will clarify what is going well, what isn’t, and what we could be doing differently. The final interview, which will take place before the Grade 10 Mathematics Provincial Exam, will serve to leave the student with a sense of where we started, how far have we gone, and where will we go from there. At the end of the final interview, I will leave students with some “Reflection Homework” that helps them synthesize the anxiety training that is taking place. I will also encourage these six students to set up appointments for informal “check-ins” as they deem appropriate.
Lastly, I will maintain a field journal throughout the semester, documenting observations from in class and summarizing my interviews (this is especially important for any spontaneous interviews that will not be audio-recorded). I will also ensure that I thoroughly check my students’ I. E. P.s (Individualized Education Plans), and make note of any anxiety related information.
Procedure
Prior to the semester’s commencement, experiment and control groups need to be determined and permissions obtained from parents. For each group, one Gifted and one Regular academic Mathematics 10 will be recruited. The sequence of the procedure, henceforth, is as follows:
- Day 1 of the semester: Students in all four classes will be given the Math Anxiety Survey. The control groups will not be surveyed again until the final day of class, but before their final exam.
- Week 1 to end of semester: The experiment groups will receive mini-lessons aimed to educate students into the causes and effects of anxiety. Teaching practices will also be altered to minimize triggers that have been shown to activate students’ anxiety. I have included an “Anti-Anxiety Tip Sheet” that I have produced in the Appendix (Figure 3). Every effort will be made to implement these theories in my teaching practice, and I will record these theories in my field journal on a daily basis.
- Day of each unit test: There are 6 unit tests in FPC Math 10. Using an anonymous, 4-point, self-developed Likert scale survey, the students will take this survey the day of each unit test. The survey, called the “Pre-Math Test Check-in,” asks questions pertaining to students’ mathematical preparedness, confidence, and overall feelings of nervousness. The rationale of this procedure is twofold. First, mathematical preparedness and confidence have been shown to be inversely related; therefore, the survey was designed to gauge these factors (Hembree, 1990). Secondly, the questions also serve to remind the students about the importance of completing practice work, doing the practice test, and reviewing the notes as part of their studying process for math. Teaching study skills to students is a key way to minimize their test anxiety (Salend, 2011).
- The day after each unit test: A quick self-reflection will be given to students with three questions to answer (see Instruments). After the first reflection, I will assess which students produced the most information-rich responses, and cross-reference those students with their math anxiety scores. Those students who provide detailed responses and who also have ranked between “moderate” to “high” (3.0/5 – 4.0/5) for math test anxiety will be approached to become part of the qualitative case study. Ideally, three students from each experiment group will be recruited. As an incentive to participate, I will reduce the weighting of tests on these students’ spreadsheets by 5%. That 5% will then be comprised of a “study participation” score.
- The week after the first unit test: The six case study students will be interviewed for the first time. My goal will be to gain insight into their math history and to find out about their personal anxiety triggers. As I have previously mentioned, a “game plan” will be created together to help these students become less anxious with their math testing.
- Mid-semester: After Chapter 3, I will conduct a check-in interview with the six case study students. I will go over their spreadsheets in the course with them in detail and see how they are feeling about the course overall. The goal will be to determine what techniques have been working for them and where a change might be needed to maximize this experience.
- End of semester: Before the Provincial final examination, I will conduct a final interview with the six case study students. The purpose will be to talk about their study strategy for the final exam, to discuss their game plan for their next course, and to determine what anti-anxiety techniques have worked the best for them. I will also be giving them a “Dear Me” assignment. This is a reflection in which they will write a letter to themselves, which will then supposedly be transported back to them at the beginning of the semester. The letter will need to convey their successes, their misses, what they are most proud of, what new strategies really worked well for them that resulted in reduced anxiety, and any other advice that they would give themselves.
- Last “teaching” day of class: Students from all four classes will take the Mathematics Anxiety Survey for the second time so as to gauge whether their overall mathematics anxiety has been reduced.
Limitations and assumptions of procedure. Only 50-60 students will be in the treatment group for this study and another 50-60 students will be in the control group, thereby restricting the generalizability of the study. The overall anxiety levels determined at the beginning and end of the semester will be using an adapted version of a survey designed to gauge test anxiety in general. The only adaptation that I made was to add the word “math” in certain places to make the survey specific to math anxiety. I am assuming that this change will not affect the validity of this survey to any great extent. As well, although the control group will not be receiving treatment from me, it is possible that the teachers in those classes will implement anti-anxiety teaching strategies that are similar to mine. This study assumes that the frequency and variety of anti-anxiety teaching strategies used by the control group teachers will be minimal and reflective to those of “the average teacher.”
Research design and analysis
Rationale of research method. Since the quantitative and qualitative components of this survey are interwoven with each other, the triangulation mixed methods design is the optimal method for my study. Research questions (a) and (c) will be addressed using the qualitative methods outlined in the procedure. Interviewees will have been specifically selected to minimize validity threats and to maximize engagement with students who demonstrate a willingness to share and reflect in a productive way. This one-on-one process will thereby allow me to be able to obtain a cornucopia of relevant information. To address research question (b), I will use the Pre-Mathematics Test surveys to quantify students’ attitudes and study habits immediately before the unit tests. By analyzing the trends in these data, I will be able to establish if the group work, combined with anti-anxiety classroom policies, actually does make a difference in those attitudes and study habits over time. As well, the initial and final Mathematics Test Anxiety Surveys will establish my baseline anxiety levels to ultimately determine if changes in classroom policies can noticeably reduce mathematics anxiety.
Limitations. The non-equivalent control group design lends itself to certain threats to its internal and external validity. Statistical regression, differential selection, and pretest-treatment interaction threats are typical in this type of design, as a consequence in large part to the non-random selection of participants. To minimize these effects where possible, I will not use students who self-report themselves as having high or low anxiety, in the qualitative component of the study, and thereby address regression issues. In my particular school, there are three levels of mathematics at the Grade 10 level: Apprenticeship and Workplace (A&W), Regular, and Gifted. Therefore, the students in my Regular Math 10 are typically void of students who are particularly challenged at math, since they tend to register in A&W math. Hence, most students in Regular math classes are relatively homogenous, and finding a control group within the school should not be an issue, thereby minimizing selection threats. To eliminate the effects of Pretest-Treatment interaction, I will administer the initial anxiety survey to participants in the first week of class. The next self-assessment of their anxiety will not occur for another two weeks, and it will utilize a different, shorter survey.
Lastly, there are also limitations to undertaking a “field experiment” as opposed to a “true experiment” that controls nearly all threats to an experiment’s validity. Since my experiment will occur in the natural classroom setting, I will not be able to control all of the external variables that could influence a student’s anxiety levels, such as personal stress and stress from other classes. As well, for this study to be reproduced, a new researcher would find it very difficult to recreate exactly the same conditions that I had in my classroom. Ultimately, by being aware of these threats, I will be able to create a study that has at least some limited generalizability.
Data collection and analysis.
- Math Anxiety Survey. Once the surveys are completed, I will determine the mean of the responses to give each student an anxiety score out of 5. I will then group the students into three categories: High Anxiety (3.7 – 5), Medium Anxiety (2.3 – 3.6) and Low Anxiety (1 – 2.2). The evenly distributed anxiety levels will categorize the dependent variable as being an “interval variable.” Since the independent variable, implementation of anti-anxiety techniques, will consider the effects on two groups, namely gifted and non-gifted, the independent variable is considered to have two levels. As well, since the same students will each undergo a pre-test and post-test, the groups that I have are categorized as “dependent” will consistent of those students whose anxiety levels have decreased little over time. Hence, the most appropriate statistical test to use for analysing the data from the Math Anxiety Survey will be the paired t-test. A significance value of 0.05 will be used to test whether or not the null hypothesis is true, where the null hypothesis is that anti-anxiety techniques will not have an effect on students’ mathematics anxiety levels.
Lastly, to compare anxiety levels between the experimental group and the control group, I will run a one-tailed t-test to determine if the treatment group exhibited less anxiety. This decision is the result of my assuming that anti-anxiety techniques will not make students more anxious.
- Pre-Math Test Check-in: The questions will be categorized in the following way:
- Preparedness and Study Skills (Questions 1 – 2*) *Q3 will not be considered in the data since it is too subjective. I will keep it in the survey, however, to emphasise the importance of reviewing notes before examinations.
- Confidence (Questions 4 – 5)
- Anxiety Levels (Question 6 -7)
Each arrow will be given a numerical value of +2, +1, -1, and -2, whereby the positive values are assigned to positive attributes, such as not feeling nervous. For each category, I will sum the total points for each student. Over time, I would hope to see the sums in each category moving towards the optimal value of +2. Scatterplots of each category over time will also be produced to see trends as the course continued. In other words, scatterplots of Preparedness versus Time, Confidence versus Time, and Anxiety versus Time will be examined. Since these surveys are anonymous, I will utilize the average score from each class. Using linear regression techniques, I will also compute the slope of the best fit line from the gifted and non-gifted classes. Lastly, to compare how the two independent groups (gifted and non-gifted) respond, I will utilize the Mann-Whitney U-test on these data because I will have one independent variable (exposure to anti-anxiety techniques), with two levels (gifted and non-gifted), with the dependent variables being “interval” in nature.
For all data analysis processes, an Excel spreadsheet will be used. In the Appendix, I have included diagrams that illustrate how the groups are assigned and the data collection techniques for the qualitative component of my study in Figure 4.
Schedule of Activities
| When | Who | What | How/Why |
| Day 1 | All 4 groups | Math Anxiety Survey | · 5-point Likert scale
· determine subgroups of students |
| Week 1 | Experiment
groups only |
Anxiety Education | · In-class mini-lessons on Anxiety 101: what is it, how it works, what can be done to help control/reduce, how my class may be different than other math classes |
| Day of each unit test | Experiment
groups only |
Pre-Math Test
Check-in |
· 4-point Likert scale
· To monitor test readiness, confidence and anxiety levels |
| Day after each unit test | Experiment
groups only |
Reflection | · What went well on the test?
· What didn’t go well? · What will they try to do differently on the next test to reduce their anxiety even more? |
| The week of the first test | 6 case study students | Initial Interview | · Individually administered
· Determine math history, anxiety triggers · Create a math “game plan”. |
| During each test | Experiment
groups only |
Anxiety coaching | · Friendly reminders of the techniques
· Assisting individuals who are leaving blanks on their tests when they actually know something |
| Mid-semester | 6 case study students | Check-in Interview | · Individually administered
· Determine where they are at with their anxiety? · Has anything changed? New triggers? · Offer strategies specific to their anxiety-reducing process |
| End of Semester | 6 case study students | Final Interview | · Individually administered
· Where are they at now? · What strategies were the most beneficial? · What will they work on for their next course? · How could this study improve? |
| Last Day of class (but before final exam) | All 4 groups | Math Anxiety Survey | · Same survey as on Day 1 |
Discussion
Significance and possible implications of research
This week, I had the pleasure of presenting the math department in my school with some of the literature in this field of study. My five colleagues initially responded to the conversation in a very positive way. That is, until I showed them the anti-anxiety tip sheet that I created that incorporates both the research I have found and teaching practices that have worked for me in the past. At one point in the conversation, a teacher said that he uses anxiety as a “motivational tool” to get his students to start handing in work! The teachers who spoke indicated that although they were in favour of reducing their students’ anxiety, that they were not prepared to change some of their anxiety causing practices, such as timed tests and publicly posting the class marks. Would they have been so rigid in their thinking if they had “proof” that these practices were detrimental?
I maintain that conducting further research in this field will promote the normalization of anxiety amongst the student population. This will in turn, encourage more students to talk about their own anxieties and to seek help in lessoning anxiety’s effects. Secondly, math educators may be apprehensive undertaking certain anxiety-reducing techniques to help their students, if they are not properly trained. This study will ideally help them execute some simple strategies in their own classes that have been already demonstrated to work and to seek out further training in this field. On the district level, superintendents may see higher graduation rates and standardized test scores in mathematics related subjects, due to an increased awareness of anti-anxiety teaching practices.
Relationships of research to literature
This study would unquestionably build on the significant research already completed on the topics of anxiety and gifted learners. Targeting the high school population, for whom the stakes have been raised, and specifically the Grade 10 level, the age at which mathematics anxiety peaks, makes a study of this nature relevant and important to many groups. Should a negative correlation be determined between anti-anxiety teaching practices and anxiety levels of students, other researchers may be inspired to conduct studies with more generalizable conditions. As well, should this correlation be determined, researchers may wish to replicate similar studies in other subject areas, beyond just mathematics.
Furthermore, findings from this study may give us a deeper understanding into the mind of the gifted learner. At a young age when the material is relatively simple, these learners have been shown to have less anxiety, however, as learning conditions change, it is not unreasonable to believe that anxiety levels do as well. I hypothesize that not only will the gifted class Grade 10 classes report higher levels of anxiety than then non-gifted peers, but they will also respond more to the treatment, due to their superior levels of cognitive ability.
In summary, mathematics anxiety exists and it is treatable. Not surprisingly, educators and those invested in education, may already possess the night light required for anxiety’s dark room. By removing social stigmas connected to mathematics anxiety, and by implementing anxiety-reducing classroom policies, anxious mathematics students may finally be able to come out from under the covers.
References
Ashcraft, M. H. (2002). Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11(5), 181-185. doi:10.1111/1467-8721.00196
Ashcraft, M. H., & Krause, J. A. (2007). Working memory, math performance, and math anxiety. Psychonomic Bulletin & Review, 14(2), 243-248. doi:10.3758/BF03194059
Chernoff, E. J., & Stone, M. (2014). An examination of math anxiety research. Gazette – Ontario Association for Mathematics, 52(4), 29.
Distin, K.(2006). Gifted children: A guide for parents and professionals. London; Philadelphia: Jessica Kingsley Publishers.
Driscoll, R. (2007). Westside Test Anxiety Scale Validation. Retrieved from ERIC database. (ED495968)
Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21(1), 33-46.
Huberty, T. J. R.(2012). Anxiety and depression in children and adolescents: Assessment, intervention, and prevention. New York: Springer. doi:10.1007/978-1-4614-3110-7
Richardson, F. C., & Suinn, R. M. (1972). The mathematics anxiety rating scale: Psychometric data. Journal of Counseling Psychology, 19(6), 551-554. doi:10.1037/h0033456
Salend, S. J. (2011). Addressing test anxiety. TEACHING Exceptional Children, 44(2), 58-68.
Schleyer, E., & Zeidner, M. (1999). Test anxiety in intellectually gifted school students. Anxiety, Stress & Coping, 12(2), 163-189. doi:10.1080/10615809908248328
Yazid, A., Baker, A., & Ishak, N. M. (2014). Depression, anxiety, stress, and adjustments among malaysian gifted learners: Implication towards school counseling provision. International Education Studies, 7(13), 6. doi:10.5539/ies.v7n13p6
Appendix
Table 1: Characteristics of Anxiety
| Cognitive | Behavioural | Physiological |
| · Concentration problems
· Memory problems · Attention problems · Oversensitivity · Problem-solving difficulties · Worry · Cognitive dysfunctions · Attribution style problems |
· Motor restlessness
· “Fidgety” · Task avoidance · Rapid speech · Erratic behaviour · Irritability · Withdrawal · Perfectionism · Lack of participation · Failing to complete tasks · Seeing easy tasks |
· Tics
· Recurrent, localized pain · Rapid heart rate · Flushing of the skin · Perspiration · Headaches · Muscle Tension · Sleeping problems · Nausea · Vomiting · Enuresis |
| Source: Huberty (2012, p. 32) |
Figure 1: Math Anxiety Survey
Math Anxiety Survey
- First and Last Name: ______________________
- Age: ______
- Is this your first attempt at Foundations/Pre-Calculus Math 10? (please circle) yes no
__ 1) The closer I am to a major math test, the harder it is for me to concentrate on the material.
__ 2) When I study math, I worry that I will not remember the material on the test.
__ 3) During important math tests, I think that I am doing poorly or that I may fail.
__ 4) I lose focus on important math tests, and I can’t remember material that I knew before the test.
__ 5) I finally remember the answer to math test questions after the test is already over.
__ 6) I worry so much before a major math test that I am too worn out to do my best on the test.
__ 7) I feel out of sorts or not really myself when I take important math tests.
__ 8) I find that my mind sometimes wanders when I am taking important math tests.
__ 9) After a math test, I worry about whether I did well enough.
__ 10) I struggle with completing math assignments, or avoid them as long as I can. I feel that whatever I do will not be good enough.
Source: Adapted from the Westside Test Anxiety Scale, http://files.eric.ed.gov/fulltext/ED495968.pdf
Table 2: Westside Anxiety Ranking Scale
| Mean Score | Math Test Anxiety Level | |
| 1.0 – 1.9
2.0 – 2.4 2.5 – 2.9 3.0 – 3.4 3.5 – 3.9 4.0 – 5.0
|
Comfortably low
Normal or Average High normal Moderately high High Extremely High
|
|
Source: Adapted from the Westside Test Anxiety Scale, http://files.eric.ed.gov/fulltext/ED495968.pdf
Figure 2: Pre-Math Test Anxiety Self-Test (self-developed)
Pre-Math Test Check-in
Code name: _________________________________
| 1. | I completed the Practice Work entirely and there were few to no errors. | << | < | > | >> | I had many errors on the Practice Work and/or I did not complete it. |
| 2. | I completed the Practice Test entirely and there were few to no errors. | << | < | > | >> | I had many errors on the Practice Test and/or I did not complete it. |
| 3. | I reviewed the notes thoroughly. | << | < | > | >> | I did not review the notes at all. |
| 4. | I am really prepared for this test. | << | < | > | >> | I am not prepared for this test at all. |
| 5. | I think I am going to do well on this test. | << | < | > | >> | I do not think this test is going to go well. |
| 6. | I think this test will reflect what I know. | << | < | > | >> | I think that I am going to blank out on what I know. |
| 7. | I am not nervous at all right now. | << | < | > | >> | I am very nervous right now. |
Figure 3: Anti-Anxiety Tip Sheet for Educators
Anti-Anxiety Math Techniques and Policies
Compiled by Dana Bjornson
Before Testing
- Identify students in your class that experience anxiety in math class. Whether or not you give a formal anxiety assessment (using a survey, for example) or simply put one or two questions on an Interest Inventory, this is the first step needed to help students. Students leaving entire portions of test blank may be suffering from anxiety and so they avoid practice and being engaged in class. Avoidance is the number one mechanism for people to use to help them “deal with” their anxieties.
- Desensitize students to their anxiety by providing many “quizzes” as opposed to, or in addition to, one large quiz. This will only be productive, though, if these quizzes are perceived as non-threatening. This is why I no longer count any quiz for marks and I have students mark their own quizzes. And no—my overall results have not suffered in the last eight years that I have not counted quizzes for marks.
- Teach study skills.
- Highly recommend that students complete their Practice Test as a mock test. This will help with the desensitization process. Ensure that your Practice Test is in the same format and from the same test bank (if you use one) that the unit test is in.
- Refrain from posting spreadsheets of the class’ scores on the wall for every student to see. Especially important in gifted classes, comparing one’s mathematically ability to others reinforces negative thoughts of inability. In Challenge, students can feel inadequate if they have 87%, when they see that 2/3 of the class is higher. Instead, handout individual interims or send e-reports home via Integrade.
- Normalize test & math anxiety by talking about it
- Talk about the science behind it and what is physiologically happening to them when they go into “fight or flight” mode
- Allow retests; explain your retest process ahead of time (the higher the stakes the higher the anxiety so if students know that it is possible to have a re-do, anxiety can be lowered).
- Remind them that they are not their scores; their self-worth is not based on their achievements. It is natural to want to avoid doing math if it is not a pleasant activity but avoidance only makes the anxiety worse in the end.
- If students have anxiety, they shouldn’t go to class early before a test. Conversations with classmates can intensify anxiety before the test even starts.
During Test (& the test itself)
- Allow students to have as much time as they need to write examinations; split test in two if needed.
- Put easy questions first (I also tell students to not let a question become a “black hole” question by having them “get mad” at the question. For example, “OK #6, I’m not going to let you bring me down right now. You suck and I’m going to ignore you until the end of the test.” This keeps students feeling that they are in control, not their anxiety.
- Consider allowing students to answer 4 out of 5 questions on the written.
- Put text boxes around all instructions. Directions, questions and answer space should be on the same page so that students do not have to flip back and forth. Do not reuse tests; allowing students to write on the test can reduce anxiety. Use bullets or numbering to present important information.
- Don’t have too many questions per page; make sure there is a lot of room for each question
- Questions that incorporate humour, novelty, and familiar names (places in the community, students’ names, your name, pop culture) can add meaning and make the test more motivating; do not embarrass or include people who object, however.
- Encourage a “memory dump” at the beginning of each test to lessen the fear of forgetting important information.
- Incorporate anti-anxiety coaching throughout test (reminders to use Data sheet, “Don’t erase unless you replace!”…).
- Look through a student’s test before taking it in—see if you can coach them through a couple of more questions. This is not to imply that you give them hints on specific processes, but talk them through the “get the ball rolling” techniques. Ex. Draw and label the diagram; look at the Data Sheet, etc.
- To counter negative thoughts towards the math, provide “Attribution Training”. This teaches students that the outcomes on their test are determined by specific events and actions on their part, as opposed to factors that are beyond their control (ex. bad luck, “teacher didn’t teach that”, and “the test was unfair”…)
- Consider having a section at the end of the test:
- I did well on this test because_____________
- I struggled on this test because____________
- The things I can do to be successful on future tests are _____________
- Encourage risk taking; discuss and learn from mistakes when those risks are taken
- Consider having a section at the end of the test:
- Ensure retests are in the same format as the original test. (As part of my retest process, I require that students come in and make all of their corrections on their original test. I keep their tests so that the tests’ validity is not compromised, however.)
References
Ashcraft, M. H. (2002). Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11(5), 181-185. doi:10.1111/1467-8721.00196
Ashcraft, M. H., & Krause, J. A. (2007). Working memory, math performance, and math anxiety. Psychonomic Bulletin & Review, 14(2), 243-248. doi:10.3758/BF03194059
Chernoff, E. J., & Stone, M. (2014). An examination of math anxiety research. Gazette – Ontario Association for Mathematics, 52(4), 29.
Distin, K.(2006). Gifted children: A guide for parents and professionals. London; Philadelphia: Jessica Kingsley Publishers.
Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21(1), 33-46.
Huberty, T. J. R.(2012). Anxiety and depression in children and adolescents: Assessment, intervention, and prevention. New York: Springer. doi:10.1007/978-1-4614-3110-7
Salend, S. J. (2011). Addressing test anxiety. TEACHING Exceptional Children, 44(2), 58-68.
Figure 4: Group assignment for quantitative component.
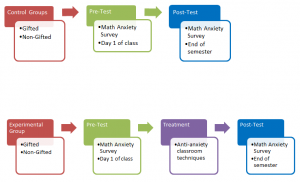
Figure 5: Data collection technique for qualitative component.
| Data
Characteristics |
Qualitative Data Collection Method | |||
| Interviews | Post-test Reflection | Reflection: “Dear Me” Letter | Field Notes/Journal | |
| Participants | 3 Gifted
3 Non-Gifted |
Everyone in treatment groups | 3 Gifted
3 Non-Gifted |
Myself |
| Text based | No | Yes | Yes | Yes |
| Audio-recorded | Yes | No | No | No |
| Anonymous | No | No | No | No |
| Incentives | Yes, less weighting on tests | No | Yes, less weighting on tests | No |
| Frequency | 3 per student | 6 | 1 | Throughout semester |
