Category Archives: assessment

January 14, 2018 · 11:25 am

Opportunity Horizon Assignment

For our first official weekly assignment, we had two options.  Either source out a new, previously unposted market or trend in the world of educational technology, or critique a preexisting post.  To read the full instructions, click here.

We all know that as soon as you buy the latest iPhone, that within the year, the next iPhone will be one the market.  Technology evolves and advances so quickly that following trends, can be very time consuming and never-ending!

For my contribution this week, I chose to source out a trend that had yet to be posted. Truth be told, I have almost no background knowledge on any emerging trends and markets in EdTechLand! Before I could even begin this assignment, I had to spend a few hours just sourcing out a trending market both, relevant to 2018 and one that I could connect with professionally.  This is what led me to Adaptive Learning (AL).

In our first week, “Adaptive Software” was presented to us as an emerging market, yet I did not quite clue in to its relevance to my practice.  Armed with a multitude of clues, I added the following comment to the AS post:

Now that I have immersed myself with the topic of “Adaptive Learning (AL)” this week, I now realize that it falls under the umbrella of “Adaptive Software”. When I initially read the Adaptive Software post, I most definitely did not appreciate its enormity and relevance to the future of education. I have always LOVED crafting and delivery lessons and so the thought of being a fulltime, “guide on the side” has never sat well with me. Knowing the affordances of AL, and knowing the adaptability of the software, has completely won me over, however. I can still put my own spins on the lessons; I can still help students with the material; my expertise is still needed, in order for students to fully thrive. My new vision is to offer one AL-pathway for those students who are interested in a new approach. Students who have traditionally experienced math-anxiety, and for some, math-trauma, could possibly experience an entirely new set of emotions, in their math classroom. This truly excites me!!!!

Having completed my analysis of AL, I have also tried to make contact with McGraw Hill Canada.  I am very interested in piloting an AL environment for a group of adventurous math students at my high school.  McGraw Hill’s software can be used on desktops, Chromebooks, and iPads, making the infrastructure a non-issue for me. What I am concerned about, is the cost of the ALEKS software.  Anything more than “free”, may be problematic! I am hoping that if I am the first adopter in the region, I may be able to secure a deal.  What I do know, with certainty, is that if I don’t make shot, I won’t score a goal…

Wish me luck!

Leave a Comment

Filed under Adaptive Learning, assessment, educational apps & programs, ETEC 522, Mathematics education

December 3, 2017 · 10:43 pm

The Non-Oppressive Mathematics Classroom: A Comprehensive Guide Towards Creating a Third Space

ETEC 521: Indigeneity, Technology, and Education

Professor: Dr. Michael Marker

December 3, 2017

Abstract

Perhaps the most commonly pondered question from frustrated mathematics students, across grades and cultures, is “When am I ever going to use this?”  For exasperated fifteen-year-old Indigenous learners, this question transcends feelings of frustration; it clashes with their entire worldview. Traditionally, mathematics has been taught entirely from a Western perspective, a mindset that is firmly rooted within the pedagogy of oppression. This essay begins to address why mathematics educators need to take a step back from strictly traditional approaches, how this shift can occur within Western high school mathematics curriculum, and how Indigenous and non-Indigenous students can mathematically thrive within a culturally inclusive, third space.

Keywords:  Indigenous, non-Indigenous, mathematics, non-oppressive, worldviews, third space, high school

 

Protocols of Place

I would like to acknowledge that this essay was written on the traditional territory of the Lkwungen people.  I would like to further acknowledge the Songhees First Nation and the Esquimalt First Nation on whose territory I live, I learn, and I work. For the purpose of situating myself within this research essay, I am a high school mathematics and physics teacher, of White settler identity— adopted into a Norwegian family at birth, and, to my knowledge, originally from Italian and English heritage. I am primarily concerned with creating an inclusive, non-oppressive learning environment for my students, reducing the effects of anxiety in the classroom, and maintaining the academic rigor required for courses in senior mathematics and physics.

Introduction

Class begins promptly at 12:20 P. M., and the agenda is on the board:

  1. Homework Questions?
  2. Hand-in homework.
  3. New section: Polynomial expansions.

Today, nobody has any questions from last night’s work.  The teacher is pleased with herself as she thinks that she must have been very effective the class before; however, this thought passes quickly, as fewer than half of her students proceed to hand in the work. She continues to teach the new lesson, as she was taught when she was in Mathematics 10.  She provides notes; students write the notes; students practice, and repeat. Her degree in mathematics has served her well—she knows what qualities the students need to succeed and to be “efficient” with their processes, as these were the qualities that she required.  If you were to ask her if she thought that she was contributing to an oppressive learning environment, she would not hesitate to say, “Absolutely not.”

The Oppressive Math Classroom

For those of us who were in high school before 2000, it is almost guaranteed that we were taught math in what is commonly called a “traditional” format, as described in the introduction. Our teachers gave notes; we wrote notes; we practiced, and were assessed. Consequently, many of us who see ourselves in the role of “math teacher” continue to teach in this traditional format. At first consideration, it may appear to be unwarranted, even outrageous, to say that learning in a traditional environment is “oppressive.”

In its most extreme form, “traditional mathematics education” can easily be equated with “math indoctrination.”  A teacher who prescribes mathematics indoctrination will provide one-sided arguments, attempt to erase learners’ differences from their processes, employ language that would pit vice against virtue, and could claim a right versus wrong way of problem-solving (Nodoushan & Pashapour, 2016).  Students in these classrooms must follow the “optimal way,” be efficient with their time, and be precise and deliberate with their strategy (Russell & Chernoff, 2012). Assessments are typically timed and performed individually, so that fully indoctrinated students will likely be successful; those who do not learn in this way risk failure, as technically this constitutes an oppressive learning environment.

In his most influential work, Pedagogy of the Oppressed, Paulo Freire describes mainstream education with the metaphor “the banking concept of education.” Although he wrote this work in 1968, it is common to find educators today possessing attitudes and following practices that imply that the teacher’s role is to merely deposit information into students as though they were receptacles. Other oppressive practices and attitudes that Freire lists include these:

  • The teacher knows everything, and the students know nothing.
  • The teacher talks, and the students listen—meekly.
  • The teacher acts and the students have the illusion of acting through the action of the teacher.
  • The teacher chooses the program content, and the students (who were not consulted) adapt to it. (p. 73, Freire)

Studies have revealed that students are less motivated in classrooms where the teacher is overly controlling, where they have fewer options for academic study, and have fewer opportunities to voice their opinions (Preston & Claypool, 2013). Should mathematics educators wish to evolve towards a non-oppressive practice, they must be prepared to loosen their academic leashes.

Also drawing from Freire’s work, Dr. Kevin Kumashiro (www.kevinkumashiro.com) has devoted his life to anti-oppressive education, amongst other forms of equalization in the classroom. Kumashiro argues that anti-oppressive teaching practices are routinely resisted when they do not fall in line with the entrenched ideations of what education is “supposed” to be.  Compacting this resistance is that, despite the good intentions of anti-oppressive sympathizers, teachers will often contribute to oppression unknowingly within their classrooms. As oppressive practices are not always identified, they may be repeated over and over, and thus experienced over and over, a cycle which results in students’ believing that there are only certain acceptable forms of identifying or thinking (Kumashiro, 2002).

On the other hand, some reformists are not simply looking at what is being done in the math classroom; rather, they are focusing on what is not being done. Stavrou and Miller maintain that, although there are many educators that recognize the disparity between Indigenous and non-Indigenous learners, there is a disconnect between what is espoused to be decolonizing, anti-oppression mathematics education and the discourse itself produced by those scholars in the field of these topics.  Often, anti-oppressive “well-meaners” will fall short in their attempts to provide decolonized education. Although they promote cultural understanding and non-Western mindsets, they neglect to address and to challenge the root causes of oppression, namely how inequalities are entrenched within our schools, and how to counter Western knowledge as superior to Indigenous ways of knowing. They also warn about the harmful effects of providing “culturally relevant mathematics” that is superficial in nature, such as teaching circular geometry by showing a medicine wheel. In circumstances where Indigenous knowledge is utilized devoid of context and meaning, not only can its use propagate stereotypes, educators risk the homogenization of Indigenous cultures and knowledge (Stavrou and Miller, 2017).  Also at risk, when simplistic versions of culturally responsive teaching are at play, is that the cultural homogenization can lead to increased instances of “othering” the non-dominant culture (Keddie, Gowlett, Mills, Monk, & Renshaw, 2012). Ultimately, practices that reinforce divisions of “us and them” are oppressive and obstructive in the creation of a safe learning environment for all. Moreover, it is critical that teachers not trivialize or decontextualize Indigenous knowledge if the learning needs of Indigenous students are to be truly valued.

Creating a Third Space

When two cultures combine and co-evolve in such a way that neither is placed as the dominant culture, but more as a new culture, some scholars describe this synthesis as representing the third space (Lipka, Sharp, Adams, & Sharp, 2007). Should there be a third space in a mathematics classroom, the new culture would have the potential to challenge existing hegemonic systems, and provide space for addressing racism and oppression, thereby creating a nurturing learning environment for all.  For the classroom to represent a third space authentically, educators must learn about the roots of oppression, such as colonization (past and present), residential schools, and racism (Stavrou & Miller, 2017).  These topics require educators to situate themselves for prolonged periods of time; considerably more time than an afternoon of Professional Development! Should teachers understand the roots of Indigenous oppression (as obvious as this will sound), non-Indigenous educators must then learn about Indigenous worldviews that can be embedded into their classroom’s third space.

Indigenous Worldviews in the Mathematics Classroom

Academic mathematics educators have many “reasons” to not embrace Indigenous worldviews within their classrooms.  These may include restrictions in teaching time, having too many learning outcomes to address, not understanding Indigenous culture or worldviews, and/or not valuing Indigenous worldviews for their subject matter.

Long before Lev Vygotsky developed his socio-cultural learning theory that focuses on the critical nature of More Knowledgeable Others (MKOs), Indigenous cultures were harnessing the wisdom of their own MKOs, namely, their elders.  Vygotskian Theory relies on MKOs to help learners flourish within their Zone of Proximal Development.  This is the space where a learner can be successful, not on their own, but with support from someone with more knowledge (John-Steiner & Mahn,1996). Elders in Indigenous communities are not only experts within their fields; they also act as conduits of culture, language, and history. Where successful examples of decolonized education have been documented, knowledge from elders is part of authentic, contextualized mathematical learning, that is far from being trivial (Lipka et al, 2007; Kawagley & Barnhardt, 1998 Preston & Claypool, 2013; Munroe, Lunney Borden, Murray Orr, Toney, & Meder, 2013).  A beautiful example of the sharing of an elder’s wisdom recently came my way on my Facebook feed. It was a video of a young girl, not more than six years old, deboning a salmon with a rather large blade.  Her mother, Margaret Neketa, was behind the camera providing encouragement, not stepping in to help physically, and allowing her daughter to make her own mistakes. At one point, the girl did make an error, and the mother calmly told her it was “okay to make mistakes”; consequently, the girl continued with even more confidence (Neketa, M., 2017). Although the little girl’s accomplishment was commendable, the magnitude of this mother’s gift of empowerment and practical, hands-on knowledge, is unmeasurable. Furthermore, how can a non-Indigenous, high school mathematics teacher draw lessons from this example of non-oppressive education?

Although academic mathematics is not traditionally “hands-on,” there are occasional opportunities that lend themselves to direct, practical experience.  Consider these examples:

  1. Surface Area: creating three-dimensional models from net diagrams.
  2. Trigonometry: using a clinometer to determine inaccessible heights.
  3. Relations and Functions: collecting actual data to graph, as opposed to using premade, tables of values.
  4. Domain and Range, Linear/Quadratic Equations, Inequalities: recreating artwork on a coordinate plane using the free, online Desmos platform (example of student work).

Although the time constraints and the number of learning outcomes to be mastered are not within an educator’s locus of control, I have found that, in my own practice, it is manageable to utilize a few practical applications within each semester. I would also reinforce the premise that to non-trivialize or decontextualize Indigenous ways of knowing, the activities should not “force” Indigeneity into the process. However, providing students with choice, such as the piece of artwork to be used in their Desmos activity, is the key because students may choose the artwork that has meaning to them.  Additionally, it is important to avoid micro-managing approaches as the students are working.  Allowing them to decide how and when they need help licenses students to have control over their learning process.  In relinquishing centralized control, educators are shifting the authority structure in their classroom, while still maintaining classroom management and the quality of the lesson content (Lipka, et al, 2007).  I do not believe that hands-on activities are possible for every lesson in academic mathematics, however, if we can occasionally weave practical applications throughout appropriate units, the result situates the learning in a non-oppressive, third space.

Collaboration with peer MKOs. Learning together via collaborative techniques is another Indigenous worldview that lends itself to mathematics in numerous ways. Vygotsky believed that MKOs could be found from all ages, not just authority figures (John-Steiner & Mahn, 1996).  In my online, ETEC 521 graduate course (Indigeneity, Technology, and Education), I watched an interview with Dr. Lee Brown, a leading expert in emotional education and creating healthy learning environments for Aboriginal learners. Here, he describes how Western culture historically promotes individualistic learning practices, whereas Indigenous cultures believe that one learns more effectively collectively.  He also maintains that, when Western classrooms fail to reflect Indigenous values, educators risk having their Indigenous students leave their classroom. What, then, can the academic mathematics teacher do both to reduce that risk and to draw from Indigenous wisdom that endorses the interconnectedness of shared knowledge?

Peer instruction. Harvard physics professor Eric Mazur is known for his alternative instructional style called peer instruction (PI).  PI is a technique in which lessons do not contain direct instruction, as the instructor’s expectation is that students will pre-read, prior to the meeting time.  Instead of direct instruction, classes include qualitative, multiple-choice questions that students vote on individually, discuss responses amongst each other, and then revote individually. The instructor moderates a class discussion that is responsive to the final voting results. Mazur explains that the success in PI is the result students’ being able to explain concepts more effectively than an experienced instructor for each other. As the peer-MKOs have only just learned the material, they have an easier time explaining from a perspective that the confused learner can more easily digest (Serious Science, 2014).

I have used a modified version of PI in my high school classroom for almost twenty years. Although I still deliver content traditionally in the form of notes, I have students discuss answers with each other throughout the lesson. Subsequently, my lessons can be noisy yet also vibrant because all students have opportunities to share their thought-processes daily. When we review material, I incorporate voting questions as directed by Mazur’s PI methodology.

Formative collaborative review. Tabletop whiteboards allow regular, small-scale review to be done collaboratively, then shown to me from across the room.  As students arrive at correct answers on their whiteboards, they become MKOs to pairs that are having difficulties.  “Snowball Math” is another technique in which students are on teams, armed with review questions that they wrote onto paper “snowballs.” For two minutes, snowballs are hurled across the room, and teams then must collaboratively solve any snowballs that were left in their zone. I just recently found this activity in a resource called the “Math First Peoples Resource Guide” (p. 22), produced by the First Nations Education Steering Committee in British Columbia. Within this guide, there is a multitude of ideas that foster third space creation.

Collaborative assessments. Mathematical assessment provides another opportunity to utilize collaborative, third space affordances. Quizzing done in a collaborative format, provides students with formative assessment, that reduces “test stress” amongst anxious mathematics learners. Allowing students the freedom to assess alone or in pairs, closed- or open-book, creates academic choice that caters to the individual needs of students. Marking their own work again shifts the responsibility towards the students, who can then obtain credit for handing in corrected work, should educators wish to record assessments.  Unit tests may also be done in a collaborative format, utilizing what is known as two-stage testing. During two-stage collaborative testing, students complete a shortened regular test individually, then in groups of four they complete the same test collaboratively.  Educators blend the two marks, say with an 80%-20% split. Students report understanding the material better, having decreased anxiety, and feeling a heightened sense of community within the class; whereas educators report higher attendance rates, lower rates of course dropouts and higher final grades (Knierim, Turner, & Davis, 2015).

As opposed to subjecting our students to repetitive forms of hegemonic oppression, these collaborative techniques repeatedly reinforce Dr. Brown’s mantra “Together, we are stronger.”  Moreover, collaborative learning practices shift the power to the students and away from the authority figure, thereby situating the learning in the third space.

Honouring multiples ways of knowing. Most high school mathematics educators have considerable experience in their field at the postsecondary level, and subsequently have an informed opinion as to how mathematical processes should optimally be done.  Optimization of process, however, is yet another practice that may be oppressive in the eyes of our students. Russell and Chernoff (2012) strike at the heart of this issue by saying, “As Indigenous students continue to struggle with mathematics teaching and learning they are concurrently struggling with yet one more aspect of this assimilation, and, thus, we are causing harm through this unethical process” (p. 116).   Traditionalists will undoubtedly take offence to the assertion that their pedagogical style is “unethical.” What is of greater concern to me, however, is that by teaching students that there is an optimal method that differs from their method, repeatedly sends the message that the students’ way of knowing is not valued. For those students who already have deep-seeded feelings of being devalued in broader contexts, rejecting their mathematical thinking may in turn perpetuate the perception that their Indigenous ways of knowing are also not valued; hence they themselves may perceive that they are not valued in our classrooms.

When multiple methodologies, in combination with cultural relevance, are presented in mathematics, students’ motivation and engagement with the mathematics increases (Kisker et al, 2011). Admittedly, in academic, high school mathematics courses, situating the mathematics within a cultural context is extremely difficult, as the mathematics is vastly learned, to perform higher levels of mathematics. Providing multiple methodologies and celebrating all forms of solutions are entirely possible in academic mathematics, however.  Expanding binomial factors, for example, can be done in a variety of ways (Table 1).

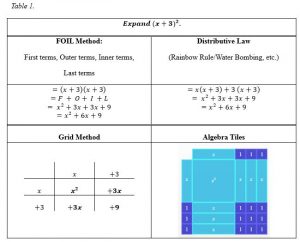
Without question, my preference is to use FOIL when expanding; however, this is of little use, should higher order polynomials be involved. Therefore, I must sometimes employ an alternative strategy. Should we require this double-barreled approach for our students as well?  In my experience, students who struggle with mathematics would prefer to learn just one strategy rather than two, so is fair to only teach to the top 50% of the class? Realistically, most students will not be taking mathematics past high school, and simply need enough academic mathematics either to graduate or possibly to enter one of countless, non-mathematics-based postsecondary programs. Moreover, it is a disservice to all our students to withhold alternative problem-solving approaches, as doing so ultimately undermines the value and creation of the third space by reinforcing a multitude of oppressive practices.

The Best of Both Worlds

Western methodologies are not without their affordances within academic mathematics contexts, and the creation of the third space allows for those affordances to remain accessible. It is also clear to me that, when educators create a third space for their students to learn within, all students benefit from this mindful effort. Helping non-Indigenous educators engage in best-practices, the case study “She Can Bother Me, and That’s Because She Cares” outlines a list of universally effective teaching strategies being used with middle school students on Baffin Island, Nunavut. Some of these strategies include the following:

  1. Adapting teaching strategies to meet the needs of the students, as opposed to having students adapt to teachers’ ways.
  2. Providing multiple learning strategies maximizes the effectiveness of students’ responses.
  3. Providing opportunities for students to voice their own strategies produces a positive learning environment.
  4. Being a caring, consistent, interested, and connected teacher who neglects student deficiencies will foster student success (Lewthwaite & McMillan, 2010).

Strict, traditional Western mathematics approaches engage in few to none of these strategies, thereby requiring Indigenous students to change, and potentially devalue, their own worldview. Sadly, this conflict of worldviews may result in the isolation of Indigenous students and their marginalization from mathematics entirely (Russell & Chernoff, 2012).

Moving forward in establishing a third space in academic mathematics classrooms, educators may follow many pathways. Providing pathways that foster resilience is a focus for some, as it is a necessary quality for students to have when developing coping strategies that mitigate stressors. York University researchers have shown that increased levels of social competency resilience and heightened appreciation of cultural identity may be fostered through Aboriginal peer mentorship programs (Rawana, Sieukaran, Nguyen, & Pitawanakwat, 2015).  In his paper entitled, “Transforming Cultural Trauma into Resilience,” Martin Brokenleg maintains that, although one can use a medicine wheel for reference, learning resilience cannot be learned from words or a poster; it must be learned through life experience. Referencing Freire’s Pedagogy of the Oppressed, Brokenleg explains that, once we are convinced that we are not good enough or smart enough, the effects of oppression are internalized and very difficult to erase from our thoughts (Brokenleg, 2012). In reality, many students entering my classes at the high school level have already internalized this harmful negativity, which I often refer to as one’s “Math Baggage.”

As a non-Indigenous educator who is mindfully making her initial steps towards the creation of a non-oppressive, third space in her mathematics classroom, I fully recognize that, in following the pedagogy described in this essay, I have merely broken the ice in considering what needs to be an ongoing journey towards a truly non-oppressive classroom.  Addressing the roots of oppression in a non-trivial way has not been addressed in this essay; nor was how to authentically embed contextualized mathematics within academic mathematics.  Nonetheless, I must follow the advice that I give to my students: a person’s not knowing how the entire solution plays out does not mean that he or she cannot at least begin to move towards a solution. Moreover, I must not be afraid to take risks and make mistakes in my learning, as I want my students to take risks and make their own mistakes in my classroom. Learning through life experience, honouring one’s identity and one’s culture, and collaboratively sharing our knowledge for the betterment of our learning community are all Indigenous worldviews that allow all students to learn at the highest levels of mathematics in a non-oppressive environment. It truly is the best of both worlds.

References
Brokenleg, M. (2012). Transforming cultural trauma into resilience. Reclaiming Children and Youth, 21(3), 9-13.
First Nations Education Steering Committee. (2011). Math First Peoples teacher resource guide. Retrieved from http://www.fnesc.ca/resources/math-first-peoples/
Freire, P. (1970). Pedagogy of the oppressed. New York, NY: The Continuum International Publishing Group Inc.
John-Steiner, V., & Mahn, H. (1996). Sociocultural approaches to learning and development: A Vygotskian framework. Educational Psychologist, 31(3), 191. doi:10.1207/s15326985ep3103&4_4
Kawagley, A.O., & Barnhardt, R. (1998). Education Indigenous to Place: Western science meets native reality. Retrieved from http://www.ankn.uaf.edu/curriculum/Articles/BarnhardtKawagley/EIP.html
Keddie, A., Gowlett, C., Mills, M., Monk, S., & Renshaw, P. (2012). Beyond culturalism: Addressing issues of indigenous disadvantage through schooling. The Australian Educational Researcher, 40(1), 91-108. doi:10.1007/s13384-012-0080-x
Kisker, E. E., Lipka, J., Adams, B. L., Rickard, A., Andrew-Ihrke, D., Yanez, E. E., & Millard, A. (2012). The potential of a culturally based supplemental mathematics curriculum to improve the mathematics performance of Alaska Native and other students. Journal for Research in Mathematics Education, 43(1), 75.
Knierim, K., Turner, H., & Davis, R. (2015). Two-stage exams improve student learning in an introductory geology course: Logistics, attendance, and grades. Journal of Geoscience Education, 63, 157-164. Retrieved from chrome-extension://oemmndcbldboiebfnladdacbdfmadadm/http://nagt-jge.org/doi/pdf/10.5408/14-051.1?code=gete-site
Kumashiro, K. K. (2002). Against repetition: Addressing resistance to anti-oppressive change in the practices of learning, teaching, supervising, and researching. Harvard Educational Review, 72(1), 67.
Lipka, J., Sharp, N., Adams, B., & Sharp, F. (2007). Creating a third space for authentic biculturalism: Examples from math in a cultural context. Journal of American Indian Education, 46(3), 94-115.
Munroe, E. A., Lunney Borden, L., Murray Orr, A. Toney, D., & Meader, J. (2013). Decolonizing aboriginal education in the 21st century. McGill Journal of Education, 48(2), 317-337. doi:10.7202/1020974ar
Munroe, E. A., Lunney Borden, L., Murray Orr, A. Toney, D., & Meader, J. (2013). Decolonizing aboriginal education in the 21st century. McGill Journal of Education, 48(2), 317-337. doi:10.7202/1020974ar
Neketa, M. (2017, July 11). My one and only [Facebook post]. Retrieved from https://www.facebook.com/margaret.neketa/posts/1640262779327006?pnref=story
Nodoushan, M. A. S. & Pashapour, A. (2016). Critical pedagogy, rituals of distinction, and true professionalism. I-Manager’s Journal of Educational Technology, 13(1), 20.
Preston, J. P., & Claypool, T. R. (2013). Motivators of educational success: Perceptions of Grade 12 Aboriginal students. Canadian Journal of Education. 36(4), 257-279.
Rawana, J. S., Sieukaran, D. D., Nguyen, H. T., & Pitawanakwat, R. (2015). Development and evaluation of a peer mentorship program for aboriginal university students. Canadian Journal of Education. 38(2), 1-34.
Russell, G. L., & Chernoff, E. J. (2013). The marginalisation of indigenous students within school mathematics and the math wars: Seeking resolutions within ethical spaces. Mathematics Education Research Journal, 25(1), 109-127. doi:10.1007/s13394-012-0064-1
Serious Science. (2014, June 18). Peer Instruction for Active Learning – Eric Mazur [Video file]. Retrieved from https://www.youtube.com/watch?v=Z9orbxoRofI
Stavrou, S. G., & Miller, D. (2017). Miscalculations: Decolonizing and anti-oppressive discourses in indigenous mathematics education. Canadian Journal of Education, 40(3), 92-122.

Leave a Comment

Filed under assessment, collaboration, ETEC 521, Indigenous culture, Peer Instruction, Vygotsky

April 2, 2017 · 11:29 am

Analysis Post: A closer look of my ETEC 533 e-Folio

Keywords from every ETEC 533 e-folio post I made:

I have always been a selfishly keen learner.

Selfish, from the perspective that I love to engage in cerebral practices that…

  1. challenge my current thinking;
  2. improve my quality of life and the quality of lives of my loved ones;
  3. keep my career choice fresh and relevant; and
  4. make me less ignorant of the issues facing society and the world, in general.

I am not entirely sure about where my lifelong quest to learn stems from, although I am certain it is not due to solely one event in my life.  Perhaps it has something to do with my parents being educators?  Perhaps I had more positive experiences in school than negative? Perhaps I am a pleaser-type— always wanting to make my teachers and parents, and now husband and children, “proud of me”? Perhaps I have a fear of appearing “stupid”?  Perhaps I just love to learn!

When looking through my e-folio posts for the course, the theme that has surfaced throughout is “student motivation”. I will further sub-categorize this theme by using the most common words from my ETEC 533 e-folio posts, shown in larger font on the above word cloud: (how we) learn and (how we) use.

Student Motivation and How We Learn

My focus early in the course was on student misconceptions. Without question, one of the most influential readings of the course was Vosniadou and Brewer’s “Mental Models of the Earth: A Study of Conceptual Change in Childhood”.  This reading, along with watching “A Private Universe”, really emphasized how students bring in their presuppositions to every learning experience and that their knowledge is situated from needing to explain the world around them (Vosniadou & Brewer, 1002). Prior to this week, I knew that students harbored misconceptions, however, not nearly to the extent that they did and why they did. Understanding that we all have an innate need to explain the world around us, whether it is scientifically based or not, has made me realize that I need to provide more opportunities within my classroom to allow students’ thinking and reasoning to be visible (Linn et al, 2002).

Throughout ETEC 533, situating and anchoring students’ learning has been a key piece that research has shown to foster students’ motivating factors.  The well-intentioned, though outdated Jasper Series week got some of us really excited to anchor learning in real life contexts.  Reading such blog posts that were titled, “Chalk and Talk are Dead” and “Goodbye Rote, Hello Anchored Instruction” exemplify this excitement to an exciting extreme. Although I will not being giving up my digital chalk anytime soon, what I have extracted from the ETEC 533 experience is that teachers of different age groups have different end goals, and hence, different pedagogical approaches, surrounding their practices.

The situated learning strategies that resonated most with me were via LfU (Learning for Use), T-GEM (Technology-enhanced: Generate, Evaluate, Modify) and embodiment. As summarized using Microsoft’s SWAY program:

All of these models naturally incorporate motivational strategies, that help engage students to want to learn.

Ultimately, students need to not only be interested in what they are learning, but they also need to have the appropriate tools in order to make that learning transpire.  Taking into account Scaffolded Knowledge Integration (SKI), in both of the activities that I have produced, incorporating the PhEt simulation for the Gravitation T-GEM and real-time data acquisition apparatus for graphical analysis, every student has an opportunity to make their learning personal and novel (Linn et al, 2002).  This concept also reinforces a key takeaway for students who were in the Spicer and Statford 2001 study analyzing the effectiveness of virtual field trips (VFT).  Students felt that by participating in the VFT, instead of a traditional lecture, that their learning had been personalized, hence they had more opportunity to engage in independent thought. With curiosity piqued (Edelson, 2000), opportunities for relationships to be generated, evaluated and modified (Khan, 2007), and interactions between the student and environment provided (Winn, 2003), self-motivation can be maximized.  In a recent post, I relayed some motivational strategies for educators to invoke:

Perhaps not if you design your practice around a few, simple motivational concepts, as outlined in the paper, “Reality versus Simulation” (Srinivasan et al, 2006):

1.       Design your lessons to “optimally challenge” your students. Like a video game, lessons shouldn’t be too difficult or too easy, for our students to engage with.

2.      Be INTERESTING. There are two key ways:

  • Weave NOVELTY into your lesson. (C+C Music Factory knows this, well.) A very smart person conducted a study that investigated K-1 students’ tendency to utilize scientific language when describing animals.  These budding, young scientists used scientific language more often when describing animals such as legless lizards and hedgehogs than when describing more common animals such as rabbits.

  • Convey a sense of IMPORTANCE and/or VALUE to what is being learned. From my own experience, ever since I began prefacing the Factoring Unit in Math 10 with, “This is the most important unit of the course” language, the unit is no longer one of the weakest units. People seem to take it more seriously when I put it on a pedestal. I also show students where I use it in my Grade 11 and 12 classes, in order to reinforce that this process is not going away any time soon.

Another key reading for myself was Winn’s “Learning in Artificial Environments: Embodiment, Embeddedness and Dynamic Adaptation” (2003).  The importance of coupling students with their environment to foster learning particularly stood out. How can we as educators capitalize on the addictive nature of video games that provide users with appropriate challenge, maximum curiosity, and opportunities to fantasize? Prior to this week, I only considered the affordances of gamification in my pedagogy.  Now, I am considering ways of using the effects of video games within my lessons.

From this post: “Activities that challenge students, pique their curiosity and provide “fruitful” new tidbits of knowledge that can assist them with future problems, are optimal, should the new knowledge wish to be adapted (Winn, 2003).”

From the same post: “As the questions would directly relate to the Vernier activity, students would be able to apply their knowledge the next day, making use of all three mechanisms for adaption of knowledge:

  1. Creating genetic algorithms: the “if-then” rules we construct when interacting with our environment and adapting our knowledge due to collecting “fruitful” information

  2. Rule Discovery: rules would have been crafted during the Vernier activity but then further entrenched by applying the rules to the Peer Instruction questions

  3. Crossover:applying the algorithms and rules in new situations could lead to rules combining into new rules for more complex situations (Winn, 2003)”

Student Motivation and How we Use

Wanting to dive into addressing student misconceptions deeper, I chose this topic as my theme for my annotated bibliography,  “Shut up and Calculate” Versus “Let’s Talk” Science Within a TELE”.   The biggest takeaway from the annotated bibliography was understanding the new roles that educators can be adopting in non-chalk-and-talk learning environments. Previously, the term “Guide on the Side” made me very uncomfortable as my interpretation of what this role entailed was limited to inquiry roles. Now, understanding the merits and dangers of using student-generated analogies (Haglund & Jeppsson, 2013) and stepwise problem-solving strategy (SPSS) (Gok, 2014), will shape my new role as “guide”.

Although I will be putting student-generated analogies and SPSS to the test in the near future, one approach that I have already adopted this semester with all three of my current classes is what I have coined as “Collaborative Quizzing”. In an attempt to create more opportunities to allow students’ thinking more visible, I now allow students to have the option of completing their quiz with a partner. This idea stemmed from our week learning about the WISE platform.  Throughout the platform, inquiry lessons require students to reflect on their learning and to provide opportunities for students to engage with each other about the topic at hand.

From this post: “Personalizing lessons within WISE, conducting class discussions, pushing students to think outside of their comfort zones and acting as the MKO (More Knowledgeable Other) at times, are all important actions and roles for educators to adopt.”

Collaborative Quizzing also came about from watching academically vulnerable students, course after course, year after year, sit through quizzes with their pencils or heads down, or with doodles of sadness strewn throughout their paper. These students will spend 20 to 30 minutes in misery, likely either negatively self-talking or in complete surrender. This is not good use of class time. As a self-described underdog, one of my goals as an educator is to help those who need the most help. So with WISE in my toolbelt and an eagerness to make class time effective, Collaborative Quizzing was born! I am particularly fascinated with the students’ feedback on the process. Overall, the feedback has been positive, and to help meet more students’ needs, I am now making the process voluntary.

As far as assessment is concerned, quizzes did not count for marks in my class, however, what I now do is require all students submit their quizzes after they have corrected their own.  I provide answer keys during the class time and upload the keys onto our Google Classroom, for those students who need more time or for those students who were away. Students receive full marks for fully corrected quizzes, as opposed to how many questions they initially got right. Increased learning interactions with peers not only build on Vygotsky theory, but also LfU theory, in that students are receiving communication directly from their MKOs to aid in the construction of knowledge (Edelson, 2000). It is theoretically possible to then immediately apply the newly constructed knowledge during the quiz and throughout the practice work that the struggling student is likely behind in.

Concluding Thoughts

Perhaps the most significant shift in my pedagogical approach to teaching math and science has been in how I utilize class time. Although five months by post-secondary standards is a very long period of time, in high school, this time is very limited.  During those five months, we teach, reinforce, provide practice time, allow for reading time, show videos, quiz, test, conduct labs, have assemblies, go on field trips, and more.  Like a bedroom closet cannot continually have pieces added to it without being dysfunctional, educators cannot continually add activities to their courses without running out of time. However, at the Grade 10 to 12 level, a reasonable expectation exists that students can and will perform some classroom responsibilities outside of class time.

With the adoption of Google Classroom, I now conduct my labs on Google Docs.  Partners can collaborate outside of class time more easily, allowing for more constructive activities to take place during class time. I have also reduced number of required practice questions with the intent of reducing the amount of in-class “worktime”, freeing up class time for more collaborative reinforcement activities.  Essentially, I am eliminating or reducing individual study activities that are in-class, in exchange for collaborative, technology-enhanced in-class activities.

Photo by Gerberkun courtesy of Imgur.

In an earlier post, I included the following image:

Motivating people to want to learn is a task that is very difficult and at times, impossible, should the approach taken be ineffective.  I do not believe that my grade levels and subject areas allow for students to pick topics that they are interested in, therefore, I need to be creative in how the material is presented and reinforced. I am very eager to take my pre-existing TELEs and make them more “T-GEM”-ized, as I did with “Conquering Mount Gravitation” and more embodied and LfU-ized, as I did with “Life on the Descoast” and “Graph Matching with Vernier”.

What is unquestionably working to my advantage in terms of motivating students to learn in my classes, is that there are not too many teachers in my school that are embracing TELEs. When students come into my class, my approaches are extremely novel and their curiosity and interest receive instant kudos—whether the lessons are effective or not. As I continue to push my personal TELE envelope, I will continue to refine and question my lessons’ effectiveness. Educators are so fortunate to have extremely user-friendly tools available to them, to make this refinement transpire. Theoretically, more educators will adopt TELEs more readily, as more of the early adopters become more fluent.

Soon, “21st Century Learners” will simply be called “Learners”– as they should be!

References
Edelson, D.C. (2001). Learning-for-use: A framework for the design of technology-supported inquiry activities. Journal of Research in Science Teaching,38(3), 355-385.
Gök, T. (2014). An investigation of students’ performance after peer instruction with stepwise problem-solving strategies. International Journal of Science and Mathematics
Haglund, J., & Jeppsson, F. (2014). Confronting conceptual challenges in thermodynamics by use of self-generated analogies. Science & Education, 23(7), 1505-1529. doi:10.1007/s11191-013-9630-5
Khan, S. (2007). Model-based inquiries in chemistry. Science Education, 91(6), 877-905.
Linn, M., Clark, D., & Slotta, J. (2003). Wise design for knowledge integration. Science Education, 87(4), 517-538.
Spicer, J., & Stratford, J. (2001). Student perceptions of a virtual field trip to replace a real field trip. Journal of Computer Assisted Learning, 17, 345-354.
Srinivasan, S., Perez, L. C., Palmer,R., Brooks,D., Wilson,K., & Fowler. D. (2006). Reality versus simulation. Journal of Science Education and Technology, 15(2), 137-141.
Vosniadou, S., & Brewer, W. F. (1992). Mental models of the earth: A study of conceptual change in childhood. Cognitive Psychology, 24(4), 535-585. doi:10.1016/0010-0285(92)90018-W
Winn, W. (2003). Learning in artificial environments: Embodiment, embeddedness, and dynamic adaptation. Technology, Instruction, Cognition and Learning, 1(1), 87-114.

 

Leave a Comment

Filed under assessment, collaboration, Constructivism, ETEC 533, Jasper Series, Learning models, LfU, Misconceptions, Peer Instruction, Situated Learning, Vernier Probeware, Vygotsky, WISE

February 20, 2017 · 10:50 pm

Collaborative Quizzing

Today, I launched a new assessment approach in my academic Math 10 and Physics 12 classes: collaborative quizzing.

I had my traditional quizzes ready to go but I had students pair up to do the quiz together. Admittedly, I have not counted quizzes for marks for almost 10 years. When Assessment for Learning approaches came to BC, we were instructed to not penalize students for practicing. Although extreme advocates for AFL interpreted this mantra as necessitating the elimination of due dates and late penalties, I personally found that this modification increased stress levels and dropped performance levels of my students. I did, however, eliminate quizzes that lowered overall grades, then quickly eliminated all quiz scores from my gradebook. Overall, students appreciate having quizzes represent a snapshot of their present knowledge, yet also not contribute to lowering their grades. Consequently, making the leap into a collaborative model, was more like a step for me.

Throughout my Masters’ journey, I have read about the merits of collaboration and social construction of learning. And although students will simply have a unit test and final exam as their solo flight assessments, my gut is telling me that this is the way to go. My main concern is for the students who are struggling with the material— how can I provide opportunities for them to increase their conceptual understanding within my short time with them in class? Students can self-quiz themselves, outside of class, should this practice be needed, whereas this collaboration time may not be as easily accessed, once the bell rings at the end of class.

Today, I had phones brought to the chalkboard or I witnessed them being stowed into backpacks. Each pair had their own quiz, along with a table top whiteboard, to get ideas out in the open. Some groups worked solo and only conversed occasionally. Other groups talked about every question in detail. When a group was unsure, I guided their understanding and sent other groups to help, when I was busy. Potentially, in this model, students harbouring misconceptions will have their issues resolved right away! I also had each student input their final answers into a Response System, so that I could gauge where everyone was at, at the end of the process, and review any questions with the class that proved to be challenging. Tomorrow, I will poll the classes to see how they felt this approach went.

If I was the student, who was not entirely sure about the concepts, I would have very much appreciated this style of non-stressful, non-punitive, low-anxiety collaborative assessment.

I am more than curious to see what they will say! …stay tuned!

Update On Post: Here is a link to the Google Spreadsheet summarizing the students’ responses from my Collaborative Quiz Survey.

March 12 Update: After absorbing the comments from the survey, I decided to allow individuals the choice of “going solo” on their quiz. Although, I tried to convince them of the merits of teaching others (being the MKO), a few students still preferred to be take on the “lone wolf” approach to their learning. The students who have fallen into this lone wolf category tend to either be on their own in class usually or are very capable students who typically are able to resolve their issues on their own. By far, the vast majority of students are fully using or partially using this time as an opportunity to work together on questions. Seeing my “strugglers” make full use of their time during a time that would otherwise be spent doodling on the back of the quiz, is reason enough to make me want to continue this assessment technique. I now have students hand in corrected quizzes that count toward Practice Work (Homework) marks. Students mark their own and are responsible for making their own corrections. Work MUST be shown and absent students can get the answer key from the Google Classroom. This process is a home run as far as I am concerned!

Leave a Comment

Filed under assessment, collaboration, ETEC 533, Vygotsky

February 12, 2017 · 6:16 pm

Further Reflections on the Jasper Series

Reading my classmates posts this week both  validated my thoughts and made me think how I could incorporate Jasper methodologies into my practice.   Now that BC Math 10 teachers have had their Provincial Exam shackles removed, there is theoretically time to weave “real world” problem solving into the course. In addition, the new curriculum is noticeably less rigorous– it appears as though for every new learning outcome that has been added, we have “lost” about three.  (Is this a good thing?  Well, that is a completely different blog post to be written…)

Reflections that I have included on classmates posts include:

  1. On Vibhu Vashisht’s post: “To respond to your question, I think that I would like to do a Jasper-esque problem at the end of my course (Foundations/Pre-Calculus 10), once the concepts have been taught and rehearsed. I think that students would really sink their teeth into a “real life” problem that involved concepts from the course and with a group dynamic, everyone at every skill level could participate. The new Math 10 curriculum has a probability component in it now, so devising a problem that incorporates a game would be very cool. Perhaps after trying it out once, I would consider having more through out my course, but I am not prepared to jump in with two feet, at this point.”

  2. On Catherine Servko’s post: “My ultimate point is that when adopting new strategies, I believe it is advisable to not let the pendulum sway to an extreme. So keep some rote learning on the basic skills— ones that are critical to continue in academic mathematics in high school and post-secondary. But then, adopt new strategies that also allow students to receive the socio-cultural, anchored learning affordances. Best of both worlds!”

  3. On Mary Sikkes’ post: “Sometimes, it is hard to NOT overthink things. I think that you should just give the Jasper approach a shot, on a relatively small scale, and then reflect on what went well and what could be adapted for next time. It is kind of like bringing in a new form of technology to your practice— it will likely not be perfect, but it gets the ball rolling, at least!”

  4. In response to  Anne’s reply on my post: “The one time, as a student in grade school, that I dreaded math, was when I clearly did not have the basic skills down pat. I was at the end of my Grade 3 and I was at my third school in that grade. I was so behind the other kids with my times table knowledge. I would feel so dumb because we would sit in groups of three with a student flashing cards and testing us. Public humiliation felt horrible! However, once I caught up in that area, I started liking math again, and really appreciated the fact that with extra effort, I could do as well as anyone. When in Grade 5, Mrs. Wong gave us a challenge to complete all of the questions in the supplemental math text, I took her up on the challenge and was the first student done (and got the first pick off of the prize table!) You could imagine that my basic, fundamental skills were automated and accurate after having completed hundreds of extra questions. I truly believe that Mrs. Wong’s competition is one of two main reasons that I went on in math in university. It allowed me to confidently attack the more difficult problems in every math class in Grade School and set me up to enjoy learning new mathematics. I appreciate that not everyone will respond to rote learning competitions, as I did. But at the end of the day, it really worked for me.”

This week, Catherine Sverko, mentioned the “grey nature” of teaching.  Becoming a “Shades of Grey Educator”, is a time-consuming and at times, overwhelming metamorphosis.  Considering each student as a whole individual, can be messy, because in order to do so, the personal qualities of the individual can not be ignored. Not every educator is prepared to “go grey”, either. A counselor who is on a temporary contact mentioned  to my colleague that she is really enjoying her time at our school because when she approaches teachers to make accommodations for her clients, the teachers actually make them happen without difficulty. Apparently, this is not always the case at other schools.

As individuals, we do not all learn at the same rate, and have the same preferred methodologies. I would speculate that perhaps more than any other subject, students bring an incredible amount of psychological baggage with them into the mathematics classroom. To think that one approach to mathematical learning is going to reach out to every student that enters your room, is optimistic at best.

My ultimate issue with adopting the Jasper methodology as one’s main pedagogical approach in mathematics is that it does not seem to give students enough repetition, to truly learn a particular process. Also, if groups are being utilized, the weaker math students risk being dragged along (happily) by the stronger math students. Can we simply sugar coat a core literacy such as mathematics, in the spirit of having students “like math” more? I do not think this is a wise approach.  To quote a colleague of mine, “In high school, we do not want to sacrifice the top 20 for the bottom 80.”  I think that classrooms that remove the rote components of mathematics are doing just that, in the name of making math “real”, and “fun”.

I am not saying that the math classroom should purely be rote learning.  I am actually quite eager to employ a Jasper style approach as an activity that brings my course to its conclusion. I think that it would serve as an engaging way to review and concurrently have students work together in teams to address a realistic situation mathematically.

As a non-purest, rote-learning advocate, I surely must ask myself, how much rote is enough? That I do not know, although with some research, I may be able to have a definitive answer.  In the meantime, I have come across The Bulletproof Musician’s blog, who espouses that if it takes about 40 repetitions to learn something, then we should aim to 100% “overlearn” (i.e. do 40 additional repetitions) for mastery.

I would estimate that in my own mathematics learning, 100% “overlearning” is about right for me. I am not the sharpest knife in the drawer, however, I am certainly not the dullest, either. For some of us, perhaps 0% “overlearning” is required, and for others, 200%.  If the ultimate goal is to have our students master the concepts, I believe our classroom approach should attempt to accommodate these differences; although who is to say there is only one way to accomplish this?  We do not learn any skills be merely watching others— if this were true, we would all play basketball like Steve Nash.   Learning skills required repetition. Repetition requires perseverance and  will. Should our students not possess both of these qualities, at what point is it OK to say that maybe a career involving academic math is not someone’s destiny? Moreover, should we continue to lower the rigor of our mathematics classes so that the “bottom 80” enjoys math class more?

What do you think?

Leave a Comment

Filed under assessment, ETEC 533, Jasper Series

October 8, 2016 · 5:54 pm

To Drill or Not to Drill…

I’m not gonna lie…  I loved this week’s reading! It took me so long to navigate through, because of taking notes, reflecting on my own practice, looking up big words that I didn’t know and rereading many parts.   I have to respond to the first Discussion question:

After reading the review of work in this area, would you encourage a ‘drill & practice’ approach to learning math, or more of a conceptual strategic-based approach? Why or why not?

I would have to argue that BOTH approaches are necessary to learning math effectively, and hence, with the least amount of personal anguish.

On the Drill side, we have the bonuses of accessing the information with very little effort via the left AG.  Maximizing the LTM that has already been established, it is akin to using a calculator as opposed to finding a strategy and processing the information using pen and paper.  Our brains can just spit the solutions out as opposed to having our brains “crank the answer out.”  It also seems as though folks who are particularly good at math are accessing their left AG, in combinations with other areas of the brain that us normal folk don’t even go near. Practice also seems to make these skills more automated and more quickly accessed.

On the strategy side, even though we are not accessing the coveted left AG, we are able to apply those strategies to “untrained” problems with much better success than those who rely solely on drilling. Applying knowledge in unfamiliar territory is a very valuable skill indeed!

Where curricula and educational fads run into trouble, in my opinion, is that when the pendulum swings towards “the new and shiniest learning strategy” (ex. Assessment for Learning, Inquiry Based Learning…), the baby is also thrown out with the educational bath water.  I refuse to believe that “old school” methodologies are complete crap and  I see real danger in going “all in” on these new strategies. Admittedly, AFL is not that new anymore.  Ontario had been using it for years before BC got its claws into it. We had Pro-D upon Pro-D, learning about AFL.  If you didn’t adopt it, you weren’t a team player— at least in my school.  So I tried it for two years, saw my GPAs plummet and saw stress sky rocket. I consequently decided to create a hybrid AFL approach to eliminate its negative effects. Did I throw it all away? No. I kept the bits I liked and turfed the bits I saw as harmful to my students’ well being.

 

Speaking of babies thrown out with bath water… Ontario is apparently in a bit of a math pickle these days since it has fully embraced the Strategy approach over the Drill.  Math scores are at an all time low.  People are freaking out—well maybe not freaking out, but you can’t ignore that Strategy based math learning, on its own, is not good for the majority of students.  An Ontario math teacher presented a GAFE conference I went to last year and I spent the entire hour wondering how it is possible for this approach to work? Her students had to answer about 8 questions per unit— when they correctly answered them, they then moved on to the next unit.  The questions were challenging, without question, but there was no repetition, no drill, no rehearsing of simple questions prior to increasingly more difficult ones.

 

Hybrid approaches.  I think this is my approach to pretty much everything in my practice! Except coffee. The coffee has got to be done one way, and it has to be done right.

Dana

PS. If you haven’t seen the movie Pi, it is about a math genius who gets hunted down by people wanting him to predict the stock market. The closing scene is him drilling into his own brain, into the left AG perhaps, so that he would no longer be able to do the bad guys’ bidding. I may have just called the police, but to each their own.

Leave a Comment

Filed under assessment, ETEC 512

September 27, 2016 · 8:23 pm

Week 3: BC Teachers are (almost) free of the shackles of Provincial Exams!

If I remember correctly, BC brought in Grade 10 exams back in 2007 (please correct me if I am wrong).   I had already been teaching for 8 years and I distinctly remember my new found frustration getting the better of me. With the new Provincials, I would have to remove the fun from both my Math and Science 10.  I had spent years creating engaging, corporative projects, only to have abandon them all so that I would have enough time to cover all of the prescribed learning outcomes.  I never taught Science 10 again— I was in a state of mourning over the course I had spent almost 10 years developing.  Why would I teach a class that only had time to superficially touch on an insane number of factoids? (Thankfully, being the only Physics teacher in the school, I had the freedom to not teach Junior Science, should I not want to.)

And here we are, nearly 10 years later. The government, in an effort to roll out their “Big Ideas”, realized that if teachers were to accommodate inquiry based learning, that the Provincials would have to go.  They are probably not sad to save a few bucks, either.  Teachers, should they choose to do so, can now go back to those inquiry based approaches, that they had long before “Big Ideas” ever came out, and hope to capitalize on facilitating more opportunities for students to learn and remember on a deeper level.

But in true government form, by plugging one hole, another hole (holes?) has formed– at least in the subject area of Mathematics. I read this week’s study with great interest.  What educator doesn’t want to learn about optimal learning and remembering conditions?  In particular, the authors, on multiple occasions, stated that educators must build on students’ background knowledge so that the new knowledge would be able to “attach” or “link” itself to the previously learned material. It is then, and only then, that higher level learning can take place.

So what’s my new problem?  It’s the “Big Ideas”.  In my opinion, “Big Ideas” need to be removed from the mathematics curriculum.  The new curriculum minimizes overlap and generates massive jumps between years of learning.  For example, combining fractions appear, disappear, then reappear. Similarly, order of operations is introduced, it vanishes, then reappears.  Skill based content, unless practiced and built upon, does erode the retrieval mechanisms, hence we risk not accessing the LTM information.

I’m not anti-Big Idea for everything.  Bring it on in Science, no question!  Expecting kids to remember information and skills from two years ago is unrealistic.

Leave a Comment

Filed under assessment, collaboration, ETEC 512, General thoughts

February 28, 2016 · 11:38 pm

Week 8: e-Rubrics r Gr8!

The question that I would like to focus on this week is:   

Are there other methods that are equally as economical, particularly in terms of instructor time, that are more suitable for assessment in a digital age?

where the “other methods” the list included were:

multiple choice tests, written essays, project work, e-portfolios, simulations and educational games

For me, this is the Holy Grail of teaching pedagogy– how to be effective as an educator and effective as an assessor.  Unless you are married to a teacher, or you are a teacher, it is likely that you have no idea how much time is consumed assessing student work.  It is the biggest time consumer of my week, now that most of my lessons are fairly under control.

Having observed my fellow Physics and Math colleagues assess, we all do not put in the same amount of time and feedback into our assessments.  It can take me over 2 hours, sometimes 3 hours, to mark 30 Physics 12 labs.  It is so time consuming that I have allowed students to hand in one copy between two lab partners, whenever I can. When I employ a rubric, I definitely cut my marking time down, and it seems as though student satisfaction with the feedback has not been comprised.  

Recently, as a GAFE adopter, I tried using Alice Keeler’s Google Sheet Rubric which allows you to adjust and weight each outcome, it totals the score, and then emails the rubric back to the student.  It also provides a space to enter additional comments.  As the students completed the entire lab on a Google Doc, I also provided comments on their labs directly.  Because I work in a high school in a district that allows students to self-consent for their FIOPPA permissions, Google Apps are at my finger tips–  I recognize, however, that this is not necessarily the case across the board.

If anyone is interested in seeing an e-rubric in action, I just made a screencast of a lab I just assessed for my Physics class.

Since this was my first time using an e-rubric, the learning curve sucked up some of the saved time, however, now that I have tried it once, I know that it will be smoother in the future.

Ironically, one of the best forms of assessment that I have introduced this year is not very high tech at all. I bought 18 individual white boards (on Clearance at London Drugs for $1 each!) and I will start most classes with collaborative warm up questions.  If a pair of students seem stuck, I send other students to peer instruct them. It is non-threatening, very efficient and NO MARKING.  I love it!

I”ve dabbled a bit with Google Forms this year, putting a “check in” on the Google Classroom.  Students receive 2 marks for participating.  Using the Add-on called Flubaroo, I can run the add-on in Sheets and immediately email students their results. Although it is pretty cool to do, I honestly think that the whiteboards are better use of class time– collaboration via peer instruction is pure magic!  The one advantage to the GF is that since I have it as an “assignment” on the GC, students who were away are still responsible for completing the check-in.  Perhaps I should have both!!! 🙂

 

1 Comment

Filed under assessment, collaboration, ETEC 565, Google Apps For Education