ETEC 521: Indigeneity, Technology, and Education
Professor: Dr. Michael Marker
December 3, 2017
Abstract
Perhaps the most commonly pondered question from frustrated mathematics students, across grades and cultures, is “When am I ever going to use this?” For exasperated fifteen-year-old Indigenous learners, this question transcends feelings of frustration; it clashes with their entire worldview. Traditionally, mathematics has been taught entirely from a Western perspective, a mindset that is firmly rooted within the pedagogy of oppression. This essay begins to address why mathematics educators need to take a step back from strictly traditional approaches, how this shift can occur within Western high school mathematics curriculum, and how Indigenous and non-Indigenous students can mathematically thrive within a culturally inclusive, third space.
Keywords: Indigenous, non-Indigenous, mathematics, non-oppressive, worldviews, third space, high school
Protocols of Place
I would like to acknowledge that this essay was written on the traditional territory of the Lkwungen people. I would like to further acknowledge the Songhees First Nation and the Esquimalt First Nation on whose territory I live, I learn, and I work. For the purpose of situating myself within this research essay, I am a high school mathematics and physics teacher, of White settler identity— adopted into a Norwegian family at birth, and, to my knowledge, originally from Italian and English heritage. I am primarily concerned with creating an inclusive, non-oppressive learning environment for my students, reducing the effects of anxiety in the classroom, and maintaining the academic rigor required for courses in senior mathematics and physics.
Introduction
Class begins promptly at 12:20 P. M., and the agenda is on the board:
- Homework Questions?
- Hand-in homework.
- New section: Polynomial expansions.
Today, nobody has any questions from last night’s work. The teacher is pleased with herself as she thinks that she must have been very effective the class before; however, this thought passes quickly, as fewer than half of her students proceed to hand in the work. She continues to teach the new lesson, as she was taught when she was in Mathematics 10. She provides notes; students write the notes; students practice, and repeat. Her degree in mathematics has served her well—she knows what qualities the students need to succeed and to be “efficient” with their processes, as these were the qualities that she required. If you were to ask her if she thought that she was contributing to an oppressive learning environment, she would not hesitate to say, “Absolutely not.”
The Oppressive Math Classroom
For those of us who were in high school before 2000, it is almost guaranteed that we were taught math in what is commonly called a “traditional” format, as described in the introduction. Our teachers gave notes; we wrote notes; we practiced, and were assessed. Consequently, many of us who see ourselves in the role of “math teacher” continue to teach in this traditional format. At first consideration, it may appear to be unwarranted, even outrageous, to say that learning in a traditional environment is “oppressive.”
In its most extreme form, “traditional mathematics education” can easily be equated with “math indoctrination.” A teacher who prescribes mathematics indoctrination will provide one-sided arguments, attempt to erase learners’ differences from their processes, employ language that would pit vice against virtue, and could claim a right versus wrong way of problem-solving (Nodoushan & Pashapour, 2016). Students in these classrooms must follow the “optimal way,” be efficient with their time, and be precise and deliberate with their strategy (Russell & Chernoff, 2012). Assessments are typically timed and performed individually, so that fully indoctrinated students will likely be successful; those who do not learn in this way risk failure, as technically this constitutes an oppressive learning environment.
In his most influential work, Pedagogy of the Oppressed, Paulo Freire describes mainstream education with the metaphor “the banking concept of education.” Although he wrote this work in 1968, it is common to find educators today possessing attitudes and following practices that imply that the teacher’s role is to merely deposit information into students as though they were receptacles. Other oppressive practices and attitudes that Freire lists include these:
- The teacher knows everything, and the students know nothing.
- The teacher talks, and the students listen—meekly.
- The teacher acts and the students have the illusion of acting through the action of the teacher.
- The teacher chooses the program content, and the students (who were not consulted) adapt to it. (p. 73, Freire)
Studies have revealed that students are less motivated in classrooms where the teacher is overly controlling, where they have fewer options for academic study, and have fewer opportunities to voice their opinions (Preston & Claypool, 2013). Should mathematics educators wish to evolve towards a non-oppressive practice, they must be prepared to loosen their academic leashes.
Also drawing from Freire’s work, Dr. Kevin Kumashiro (www.kevinkumashiro.com) has devoted his life to anti-oppressive education, amongst other forms of equalization in the classroom. Kumashiro argues that anti-oppressive teaching practices are routinely resisted when they do not fall in line with the entrenched ideations of what education is “supposed” to be. Compacting this resistance is that, despite the good intentions of anti-oppressive sympathizers, teachers will often contribute to oppression unknowingly within their classrooms. As oppressive practices are not always identified, they may be repeated over and over, and thus experienced over and over, a cycle which results in students’ believing that there are only certain acceptable forms of identifying or thinking (Kumashiro, 2002).
On the other hand, some reformists are not simply looking at what is being done in the math classroom; rather, they are focusing on what is not being done. Stavrou and Miller maintain that, although there are many educators that recognize the disparity between Indigenous and non-Indigenous learners, there is a disconnect between what is espoused to be decolonizing, anti-oppression mathematics education and the discourse itself produced by those scholars in the field of these topics. Often, anti-oppressive “well-meaners” will fall short in their attempts to provide decolonized education. Although they promote cultural understanding and non-Western mindsets, they neglect to address and to challenge the root causes of oppression, namely how inequalities are entrenched within our schools, and how to counter Western knowledge as superior to Indigenous ways of knowing. They also warn about the harmful effects of providing “culturally relevant mathematics” that is superficial in nature, such as teaching circular geometry by showing a medicine wheel. In circumstances where Indigenous knowledge is utilized devoid of context and meaning, not only can its use propagate stereotypes, educators risk the homogenization of Indigenous cultures and knowledge (Stavrou and Miller, 2017). Also at risk, when simplistic versions of culturally responsive teaching are at play, is that the cultural homogenization can lead to increased instances of “othering” the non-dominant culture (Keddie, Gowlett, Mills, Monk, & Renshaw, 2012). Ultimately, practices that reinforce divisions of “us and them” are oppressive and obstructive in the creation of a safe learning environment for all. Moreover, it is critical that teachers not trivialize or decontextualize Indigenous knowledge if the learning needs of Indigenous students are to be truly valued.
Creating a Third Space
When two cultures combine and co-evolve in such a way that neither is placed as the dominant culture, but more as a new culture, some scholars describe this synthesis as representing the third space (Lipka, Sharp, Adams, & Sharp, 2007). Should there be a third space in a mathematics classroom, the new culture would have the potential to challenge existing hegemonic systems, and provide space for addressing racism and oppression, thereby creating a nurturing learning environment for all. For the classroom to represent a third space authentically, educators must learn about the roots of oppression, such as colonization (past and present), residential schools, and racism (Stavrou & Miller, 2017). These topics require educators to situate themselves for prolonged periods of time; considerably more time than an afternoon of Professional Development! Should teachers understand the roots of Indigenous oppression (as obvious as this will sound), non-Indigenous educators must then learn about Indigenous worldviews that can be embedded into their classroom’s third space.
Indigenous Worldviews in the Mathematics Classroom
Academic mathematics educators have many “reasons” to not embrace Indigenous worldviews within their classrooms. These may include restrictions in teaching time, having too many learning outcomes to address, not understanding Indigenous culture or worldviews, and/or not valuing Indigenous worldviews for their subject matter.
Long before Lev Vygotsky developed his socio-cultural learning theory that focuses on the critical nature of More Knowledgeable Others (MKOs), Indigenous cultures were harnessing the wisdom of their own MKOs, namely, their elders. Vygotskian Theory relies on MKOs to help learners flourish within their Zone of Proximal Development. This is the space where a learner can be successful, not on their own, but with support from someone with more knowledge (John-Steiner & Mahn,1996). Elders in Indigenous communities are not only experts within their fields; they also act as conduits of culture, language, and history. Where successful examples of decolonized education have been documented, knowledge from elders is part of authentic, contextualized mathematical learning, that is far from being trivial (Lipka et al, 2007; Kawagley & Barnhardt, 1998 Preston & Claypool, 2013; Munroe, Lunney Borden, Murray Orr, Toney, & Meder, 2013). A beautiful example of the sharing of an elder’s wisdom recently came my way on my Facebook feed. It was a video of a young girl, not more than six years old, deboning a salmon with a rather large blade. Her mother, Margaret Neketa, was behind the camera providing encouragement, not stepping in to help physically, and allowing her daughter to make her own mistakes. At one point, the girl did make an error, and the mother calmly told her it was “okay to make mistakes”; consequently, the girl continued with even more confidence (Neketa, M., 2017). Although the little girl’s accomplishment was commendable, the magnitude of this mother’s gift of empowerment and practical, hands-on knowledge, is unmeasurable. Furthermore, how can a non-Indigenous, high school mathematics teacher draw lessons from this example of non-oppressive education?
Although academic mathematics is not traditionally “hands-on,” there are occasional opportunities that lend themselves to direct, practical experience. Consider these examples:
- Surface Area: creating three-dimensional models from net diagrams.
- Trigonometry: using a clinometer to determine inaccessible heights.
- Relations and Functions: collecting actual data to graph, as opposed to using premade, tables of values.
- Domain and Range, Linear/Quadratic Equations, Inequalities: recreating artwork on a coordinate plane using the free, online Desmos platform (example of student work).
Although the time constraints and the number of learning outcomes to be mastered are not within an educator’s locus of control, I have found that, in my own practice, it is manageable to utilize a few practical applications within each semester. I would also reinforce the premise that to non-trivialize or decontextualize Indigenous ways of knowing, the activities should not “force” Indigeneity into the process. However, providing students with choice, such as the piece of artwork to be used in their Desmos activity, is the key because students may choose the artwork that has meaning to them. Additionally, it is important to avoid micro-managing approaches as the students are working. Allowing them to decide how and when they need help licenses students to have control over their learning process. In relinquishing centralized control, educators are shifting the authority structure in their classroom, while still maintaining classroom management and the quality of the lesson content (Lipka, et al, 2007). I do not believe that hands-on activities are possible for every lesson in academic mathematics, however, if we can occasionally weave practical applications throughout appropriate units, the result situates the learning in a non-oppressive, third space.
Collaboration with peer MKOs. Learning together via collaborative techniques is another Indigenous worldview that lends itself to mathematics in numerous ways. Vygotsky believed that MKOs could be found from all ages, not just authority figures (John-Steiner & Mahn, 1996). In my online, ETEC 521 graduate course (Indigeneity, Technology, and Education), I watched an interview with Dr. Lee Brown, a leading expert in emotional education and creating healthy learning environments for Aboriginal learners. Here, he describes how Western culture historically promotes individualistic learning practices, whereas Indigenous cultures believe that one learns more effectively collectively. He also maintains that, when Western classrooms fail to reflect Indigenous values, educators risk having their Indigenous students leave their classroom. What, then, can the academic mathematics teacher do both to reduce that risk and to draw from Indigenous wisdom that endorses the interconnectedness of shared knowledge?
Peer instruction. Harvard physics professor Eric Mazur is known for his alternative instructional style called peer instruction (PI). PI is a technique in which lessons do not contain direct instruction, as the instructor’s expectation is that students will pre-read, prior to the meeting time. Instead of direct instruction, classes include qualitative, multiple-choice questions that students vote on individually, discuss responses amongst each other, and then revote individually. The instructor moderates a class discussion that is responsive to the final voting results. Mazur explains that the success in PI is the result students’ being able to explain concepts more effectively than an experienced instructor for each other. As the peer-MKOs have only just learned the material, they have an easier time explaining from a perspective that the confused learner can more easily digest (Serious Science, 2014).
I have used a modified version of PI in my high school classroom for almost twenty years. Although I still deliver content traditionally in the form of notes, I have students discuss answers with each other throughout the lesson. Subsequently, my lessons can be noisy yet also vibrant because all students have opportunities to share their thought-processes daily. When we review material, I incorporate voting questions as directed by Mazur’s PI methodology.
Formative collaborative review. Tabletop whiteboards allow regular, small-scale review to be done collaboratively, then shown to me from across the room. As students arrive at correct answers on their whiteboards, they become MKOs to pairs that are having difficulties. “Snowball Math” is another technique in which students are on teams, armed with review questions that they wrote onto paper “snowballs.” For two minutes, snowballs are hurled across the room, and teams then must collaboratively solve any snowballs that were left in their zone. I just recently found this activity in a resource called the “Math First Peoples Resource Guide” (p. 22), produced by the First Nations Education Steering Committee in British Columbia. Within this guide, there is a multitude of ideas that foster third space creation.
Collaborative assessments. Mathematical assessment provides another opportunity to utilize collaborative, third space affordances. Quizzing done in a collaborative format, provides students with formative assessment, that reduces “test stress” amongst anxious mathematics learners. Allowing students the freedom to assess alone or in pairs, closed- or open-book, creates academic choice that caters to the individual needs of students. Marking their own work again shifts the responsibility towards the students, who can then obtain credit for handing in corrected work, should educators wish to record assessments. Unit tests may also be done in a collaborative format, utilizing what is known as two-stage testing. During two-stage collaborative testing, students complete a shortened regular test individually, then in groups of four they complete the same test collaboratively. Educators blend the two marks, say with an 80%-20% split. Students report understanding the material better, having decreased anxiety, and feeling a heightened sense of community within the class; whereas educators report higher attendance rates, lower rates of course dropouts and higher final grades (Knierim, Turner, & Davis, 2015).
As opposed to subjecting our students to repetitive forms of hegemonic oppression, these collaborative techniques repeatedly reinforce Dr. Brown’s mantra “Together, we are stronger.” Moreover, collaborative learning practices shift the power to the students and away from the authority figure, thereby situating the learning in the third space.
Honouring multiples ways of knowing. Most high school mathematics educators have considerable experience in their field at the postsecondary level, and subsequently have an informed opinion as to how mathematical processes should optimally be done. Optimization of process, however, is yet another practice that may be oppressive in the eyes of our students. Russell and Chernoff (2012) strike at the heart of this issue by saying, “As Indigenous students continue to struggle with mathematics teaching and learning they are concurrently struggling with yet one more aspect of this assimilation, and, thus, we are causing harm through this unethical process” (p. 116). Traditionalists will undoubtedly take offence to the assertion that their pedagogical style is “unethical.” What is of greater concern to me, however, is that by teaching students that there is an optimal method that differs from their method, repeatedly sends the message that the students’ way of knowing is not valued. For those students who already have deep-seeded feelings of being devalued in broader contexts, rejecting their mathematical thinking may in turn perpetuate the perception that their Indigenous ways of knowing are also not valued; hence they themselves may perceive that they are not valued in our classrooms.
When multiple methodologies, in combination with cultural relevance, are presented in mathematics, students’ motivation and engagement with the mathematics increases (Kisker et al, 2011). Admittedly, in academic, high school mathematics courses, situating the mathematics within a cultural context is extremely difficult, as the mathematics is vastly learned, to perform higher levels of mathematics. Providing multiple methodologies and celebrating all forms of solutions are entirely possible in academic mathematics, however. Expanding binomial factors, for example, can be done in a variety of ways (Table 1).
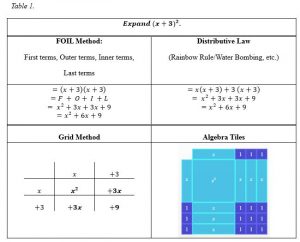
Without question, my preference is to use FOIL when expanding; however, this is of little use, should higher order polynomials be involved. Therefore, I must sometimes employ an alternative strategy. Should we require this double-barreled approach for our students as well? In my experience, students who struggle with mathematics would prefer to learn just one strategy rather than two, so is fair to only teach to the top 50% of the class? Realistically, most students will not be taking mathematics past high school, and simply need enough academic mathematics either to graduate or possibly to enter one of countless, non-mathematics-based postsecondary programs. Moreover, it is a disservice to all our students to withhold alternative problem-solving approaches, as doing so ultimately undermines the value and creation of the third space by reinforcing a multitude of oppressive practices.
The Best of Both Worlds
Western methodologies are not without their affordances within academic mathematics contexts, and the creation of the third space allows for those affordances to remain accessible. It is also clear to me that, when educators create a third space for their students to learn within, all students benefit from this mindful effort. Helping non-Indigenous educators engage in best-practices, the case study “She Can Bother Me, and That’s Because She Cares” outlines a list of universally effective teaching strategies being used with middle school students on Baffin Island, Nunavut. Some of these strategies include the following:
- Adapting teaching strategies to meet the needs of the students, as opposed to having students adapt to teachers’ ways.
- Providing multiple learning strategies maximizes the effectiveness of students’ responses.
- Providing opportunities for students to voice their own strategies produces a positive learning environment.
- Being a caring, consistent, interested, and connected teacher who neglects student deficiencies will foster student success (Lewthwaite & McMillan, 2010).
Strict, traditional Western mathematics approaches engage in few to none of these strategies, thereby requiring Indigenous students to change, and potentially devalue, their own worldview. Sadly, this conflict of worldviews may result in the isolation of Indigenous students and their marginalization from mathematics entirely (Russell & Chernoff, 2012).
Moving forward in establishing a third space in academic mathematics classrooms, educators may follow many pathways. Providing pathways that foster resilience is a focus for some, as it is a necessary quality for students to have when developing coping strategies that mitigate stressors. York University researchers have shown that increased levels of social competency resilience and heightened appreciation of cultural identity may be fostered through Aboriginal peer mentorship programs (Rawana, Sieukaran, Nguyen, & Pitawanakwat, 2015). In his paper entitled, “Transforming Cultural Trauma into Resilience,” Martin Brokenleg maintains that, although one can use a medicine wheel for reference, learning resilience cannot be learned from words or a poster; it must be learned through life experience. Referencing Freire’s Pedagogy of the Oppressed, Brokenleg explains that, once we are convinced that we are not good enough or smart enough, the effects of oppression are internalized and very difficult to erase from our thoughts (Brokenleg, 2012). In reality, many students entering my classes at the high school level have already internalized this harmful negativity, which I often refer to as one’s “Math Baggage.”
As a non-Indigenous educator who is mindfully making her initial steps towards the creation of a non-oppressive, third space in her mathematics classroom, I fully recognize that, in following the pedagogy described in this essay, I have merely broken the ice in considering what needs to be an ongoing journey towards a truly non-oppressive classroom. Addressing the roots of oppression in a non-trivial way has not been addressed in this essay; nor was how to authentically embed contextualized mathematics within academic mathematics. Nonetheless, I must follow the advice that I give to my students: a person’s not knowing how the entire solution plays out does not mean that he or she cannot at least begin to move towards a solution. Moreover, I must not be afraid to take risks and make mistakes in my learning, as I want my students to take risks and make their own mistakes in my classroom. Learning through life experience, honouring one’s identity and one’s culture, and collaboratively sharing our knowledge for the betterment of our learning community are all Indigenous worldviews that allow all students to learn at the highest levels of mathematics in a non-oppressive environment. It truly is the best of both worlds.

