[previous] [next]
Question
Using only the ratio test, determine whether or not the series
converges, diverges, or yields no conclusion.
Complete Solution
Applying the ratio test yields
Since the limit equals 
, the ratio test tells us that the series converges.
Explanation of Each Step
Step (1)
To apply the ratio test, we must evaluate the limit
In our problem, we have
and we substitute them into our limit.
Step (2)
In Step (2), we use a little algebraic manipulation to make things easier to look at
Step (3)
Step (3) uses a property of absolute values. Recall that for real numbers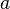 
and 
,
Step (4)
Step (4) uses a property of limits values. Recall that for functions 
and 
, 
that
Step (5)
Here we evaluate a limit:
Step (6)
Some algebraic manipulation helps us see how we can simplify our problem. Recall that, using laws of exponentials, that for real numbers 
, that
so
[previous] [next]
