Contrapositive Example with Sets

Statement A

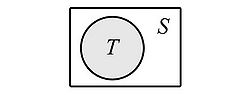
Suppose we have a set, S, and that T is a subset of S, as shown in the diagram below.

The set T is a subset of set S".

If an element y is in T, then y must also be in S, because T, is a subset of S. Let's refer to this as Statement A:

A: If an element y is in T, then y is in S.

Let the contrapositive of Statement A be Statement B,

B: If an element, y, is not in S, then it cannot be in T.

The blue area is the area not in S. The blue area cannot be in T.

Is Statement B true? Suppose we have a representative element y that is not in set S.

The black dot, y, is not in S, and therefore cannot be in T.

Since set T is inside set S, y cannot be in T. Statement B must be true.

Since set T is a subset of S, any element that is not in S cannot be in T. Otherwise, T would not be a subset of S. So Statement B follows from A.

Suppose now that we were only given Statement B:

B: If an element, y, is not in S, then it cannot be in T

From this statement we can derive Statement A:

if an element, y, that is not in S cannot be in T, then T must be a subset of S.
if T is a subset of S, then any element that is in T, must also be in S, which is Statement A.

Since Statement A follows from B, and B follows from A, these two statements are equivalent. That is, one statement implies the other.

In general, if one of the two statements are true, then the other must be true (a proof is beyond what is required for the ISM).