In previous lessons, we defined the concept of the convergence of an infinite series: the infinite series
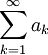
converges if and only if the limit
exists. As was mentioned, it can be very difficult to apply this limit directly, leading us to the question: is there an easier way to determine if an infinite series converges or diverges?
Examples
Consider for example
or perhaps
There might be a way of finding an explicit formula for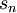 
for these series, and with these formula we may be able to use the definition of convergence directly to establish whether or not these series converge.
But, there is an easier way that quickly tells us that they do not. We can use the divergence test.
