Example: {rⁿ}

Example

Determine the values of r so that the sequence

is convergent.

Complete Solution

We can solve this problem by considering cases for the value of r.

Case 1

If r > 1, then  rⁿ tends to infinity as n tends to infinity. The sequence is divergent in this case.

Case 2

If r= 1, then

so the sequence is convergent for this case.

Case 3

If , then

so the sequence is convergent for this case.

Case 4

If , then

does not exist, so the sequence is divergent for this case.

Case 5

If , then  tends to negative infinity as 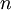does not tend to a single finite number. The sequence is divergent in this case.

Summary

Therefore, the sequence  is convergent when .

Explanation of Each Step

Case 1

Consider the case when . Then our sequence becomes

which tends to infinity.

Case 2

Here we are using a fundamental property of limits, that the limit of a constant equals that constant:

for any constant and .

Case 3

Consider the case when . Then our sequence becomes

which tends to zero.

Similarly, if  . Then our sequence becomes

which also tends to zero.

Case 4

In this case, we have the sequence

As 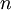approaches infinity the sequence does not approach a unique value, so the limit does not exist.

Case 5

This case is similar to Case 1. Consider the case when . Then our sequence becomes

The terms alternate between positive and negative numbers, and do not tend to a single finite number.