Final Notes on Harmonic and Telescoping Series

A Slightly More General Harmonic Series Form

We were able to show that

is divergent. It can be shown that

is also divergent, where 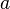is any real number. Observe that

The first sum is a constant, while the second sum is the harmonic series, which is divergent.

General Form of a Telescoping Series

One might ask how to identify an infinite telescoping series. It may seem a bit obvious, but for the sake of completeness, a telescoping series could have the form

where integers 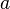and satisfy . Indeed, one could imagine more complicated forms of telescoping series, but for our purposes, this will be sufficient. Students will only need to be familiar with this form of the telescoping series.