Geometric Series Example

Example

Determine if the following series is convergent, and if so, find its sum:

Complete Solution

The sum of the series is therefore 3/5.

Explanation of Each Step

Step (1)

We first rewrite the problem so that the summation starts at one and is in the familiar form of a geometric series, whose general form is

After bringing the negative one and the three fifths together, we see that our given infinite series is geometric with common ratio -3/5.

For a geometric series to be convergent, its common ratio must be between -1 and +1, which it is, and so our infinite series is convergent.

We must now compute its sum.

Step (2)

The given series

starts the summation at , so we shift the index of summation by one:

Our sum is now in the form of a geometric series with a = 1, r = -2/3. Since |r| < 1, the series converges, and its sum is

Step (3)

In Step (3) we applied the formula for the sum of a geometric series:

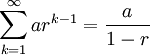
This formula was derived in a previous section of this lesson.