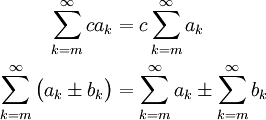Previous: Sigma Notation Terminology
Next: Changing Summation Limits
The Properties
As one might expect, sigma notation follows the following properties.
| Theorem: Sigma Notation Properties |
|---|
Suppose  and  are functions of  ,  is any integer, and  is any real number. Then
|
For these properties, we also require the infinite sums to exist. We will discuss what it means for an infinite sum to exist in the next lesson. These properties are easy to prove if we can write out the sums without the sigma notation.
Simple Example
The infinite sum
can be written as
Certainly, decomposing the combined sum in (1) into two sums in (2) does not give us a simpler representation. But this decomposition would allow us to more easily perform the convergence tests that we introduce in later lessons.
Previous: Sigma Notation Terminology
Next: Changing Summation Limits
