Next: Convergence of Infinite Sequences
An infinite sequence of numbers is an ordered list of numbers. Examples could include
- the positive integers: 1, 2, 3, 4, ...
- the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, ...
- a sequence defined by Newton's Method:
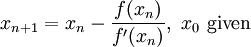
For the purposes of the ISM, we will only consider sequences with real numbers.
Notation
We often will use the notation
to denote a general infinite sequence, whose terms are a1, a2, a3, ... . For example, in the case of the Fibonacci sequence,
Key Questions for This Lesson
Given a sequence of numbers, , we could ask the following questions:
- How do we know if the infinite sequence converges to a finite number?
- If the given infinite sum does yield a finite number, what is it?
These two questions and their answers are the subject of this lesson.
Examples
If we consider examples 1 and 2 above, then we can see that by inspection, the sequences does not converge to a finite number because successive terms in the sequences are increasing.
However in some cases, it can be more difficult to establish whether the sequence converges. Depending on the form of 
in Example 3 above (Newton's Method), it can be difficult or impossible for us to determine whether this sequence converges by inspection. Indeed, we need a more rigorous method to establish convergence, which we will explore next.
Next: Convergence of Infinite Sequences
