Absolute Convergence Implies Convergence

Previous: Absolute Convergence

Next: Proof of the Ratio Test

The ratio test uses the following theorem.

Theorem: Absolute Convergence Implies Convergence
If the infinite series $\text{[math]}$ is absolutely convergent, then it is convergent.

Theorem: Absolute Convergence Implies Convergence

If the infinite series

$\text{[math]}$

is absolutely convergent, then it is convergent.

Proof

By assumption,

$\text{[math]}$

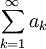
is absolutely convergent, meaning that

$\text{[math]}$

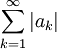
is convergent. Therefore,

$\text{[math]}$

is also convergent. Since

$\text{[math]}$

then

$\text{[math]}$

is convergent by the comparison test (the comparison can be found in most introductory calculus books that cover infinite series).

Finally,

$\text{[math]}$

must also be convergent because it is the difference of two convergent series.

So What?

Simply put, if we can show that an infinite series is absolutely convergent, then we know that it is convergent. Sometimes, it's easier to show that a series is absolutely convergent than it is to show that it is convergent.

Previous: Absolute Convergence

Next: Proof of the Ratio Test

Proof

So What?

Leave a Reply Cancel reply

Site Map