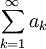Back to The Divergence Test

Back to the Divergence Test

The given statement

If the series

is convergent, then the limit

equals zero

is certainly true. We were able to prove it in our lesson on the Divergence Test. We can construct the contrapositive of this statement by reversing the conditions and making them false:

If the limit

is not zero, then the series

is not convergent.

The contrapositive statement is the Divergence Test.

Now, we know that the contrapositive of a given statement is true if the given statement is true.

But the original statement is true, so the contrapositive is also true. That is, the Divergence Test requires no proof, because it is the contrapositive of a statement that is true.