[previous] [next]
There are certain forms of infinite series that are frequently encountered in mathematics. The following example

for constants 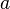 and
and 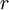 is known as the geometric series. The convergence of this series is determined by the constant
is known as the geometric series. The convergence of this series is determined by the constant  , which is the common ratio.
, which is the common ratio.
| Theorem: Convergence of the Geometric Series |
|---|
Let 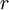 and and 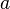 be real numbers. Then the geometric series be real numbers. Then the geometric series
converges if |
Proof
To prove the above theorem and hence develop an understanding the convergence of this infinite series, we will find an expression for the partial sum, 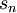 , and determine if the limit as
, and determine if the limit as 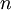 tends to infinity exists. We will further break down our analysis into two cases.
tends to infinity exists. We will further break down our analysis into two cases.
Case 1: 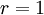
If 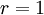 , then the partial sum
, then the partial sum 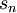 becomes
becomes

So as

we have that
 .
.
Hence, the geometric series diverges if r = 1.
Case 2: 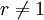
A short derivation for a compact expression for 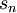 will be useful. First note that
will be useful. First note that

The second equation is the first equation multiplied by 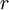 . Subtracting these two equations yields
. Subtracting these two equations yields

Using this result, we see that:
- if
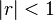 , then as n → ∞, sn → a/(1-r)
, then as n → ∞, sn → a/(1-r)
- if
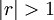 , then as n → ∞, sn → ∞
, then as n → ∞, sn → ∞
- if
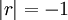 , then the series is divergent by the Divergence Test (which we cover in a lesson in Unit 2)
, then the series is divergent by the Divergence Test (which we cover in a lesson in Unit 2)
[previous] [next]


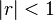 , and otherwise diverges.
, and otherwise diverges.
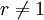
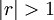 , then as n → ∞, sn → ∞
, then as n → ∞, sn → ∞
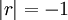 , then the series is divergent by the Divergence Test (which we cover in a lesson in Unit 2)
, then the series is divergent by the Divergence Test (which we cover in a lesson in Unit 2)

