Next: Videos on Telescoping and Harmonic Series
Recall that given a geometric series, we were able to establish convergence by deriving an expression for the partial sum,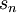 
, and by determining the value of
However, given a general infinite sum, this approach is not always convenient and sometimes impossible because we cannot always find an expression for 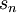. But there is another class of infinite series where this approach is feasible.
Consider the following example. Suppose we would like to determine whether the series
converges, and determine its sum. One approach is to use the definition of convergence, which requires an expression for the partial sum, 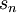. We see that
by using partial fractions. Expanding the sum yields
Rearranging the brackets, we see that the terms in the infinite sum cancel in pairs, leaving only the first and lasts terms.
Hence,
Therefore, by the definition of convergence for infinite series, the above telescopic series converges and is equal to 1.
Next: Videos on Telescoping and Harmonic Series
