[previous] [next]
The following theorem will yield the divergence test.
| Theorem 1 |
|---|
|
If the infinite series
is convergent, then
|
Proof of Theorem 1
The proof of this theorem can be found in most introductory calculus textbooks that cover the divergence test and is supplied here for convenience. Let the partial sum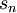 
be
Then
and 
By assumption, an is convergent, so the sequence {sn} is convergent (using the definition of a convergent infinite series). Let the number S be given by
Since n-1 also tends to infinity as n tends to infinity, we also have
Finally,
Thus, if
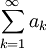
is convergent, then
as required.
[previous] [next]
