The Power Series

Indeed, a there is a more general representation for the series we introduced on the previous page:

The more general representation is given by the following definition.

What Is A Power Series?

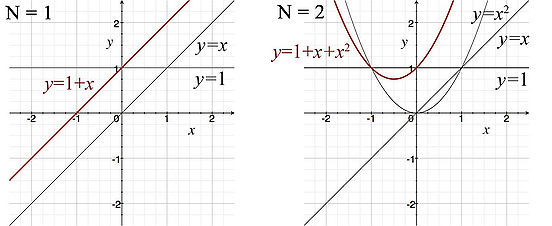
It may help to consider a simple example with partial sums. Let's take the case where a_k = 1, and c = 0, which gives us

If we let N = 1, then we have a polynomial of order 1

If we take N = 2, then we have a polynomial of order 2

Similarly, with N = 3, then we would obtain a polynomial of order 3

In the limit as N goes to infinity, we obtain a power series.

The figure below provides a graphical explanation of what a power series is: an infinite polynomial.

This diagram helps to demonstrate the idea of a what a power series is. We consider the simple case when a_k = 1, and c = 0. Using partial sums, the left corresponds to N = 1, and the right to N = 2. As we let N go to infinity, we obtain a power series.